Ангелина Яковлева - Ответы на экзаменационные билеты по эконометрике

Можно сделать вывод, что одной из основных причин присутствия мультиколлинеарности в модели множественной регрессии является плохая матрица факторных переменных Х .

Чем сильнее мультиколлинеарность факторных переменных, тем менее надежной является оценка распределения суммы объясненной вариации по отдельным факторам с помощью метода наименьших квадратов.

Включение в модель мультиколлинеарных факторов нежелательно по нескольким причинам:

1) основная гипотеза о незначимости коэффициентов множественной регрессии может подтвердиться, но сама модель регрессии при проверке с помощью F-критерия оказывается значимой, что говорит о завышенной величине коэффициента множественной корреляции;

2) полученные оценки коэффициентов модели множественной регрессии могут быть неоправданно завышены или иметь неправильные знаки;

3) добавление или исключение из исходных данных одного-двух наблюдений оказывает сильное влияние на оценки коэффициентов модели;

4) мультиколлинеарные факторы, включённые в модель множественной регрессии, способны сделать её непригодной для дальнейшего применения.

Конкретных методов обнаружения мультиколлинеарности не существует, а принято применять ряд эмпирических приёмов. В большинстве случаев множественный регрессионный анализ начинается с рассмотрения корреляционной матрицы факторных переменных R или матрицы ( ХТХ ).

Корреляционной матрицей факторных переменныхназывается симметричная относительно главной диагонали матрица линейных коэффициентов парной корреляции факторных переменных:

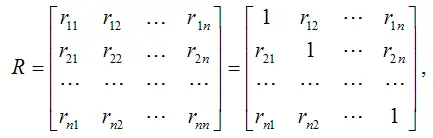
где rij – линейный коэффициент парной корреляции между i -м и j -ым факторными переменными,

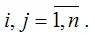
На диагонали корреляционной матрицы находятся единицы, потому что коэффициент корреляции факторной переменной с самой собой равен единице.

При рассмотрении данной матрицы с целью выявления мультиколлинеарных факторов руководствуются следующими правилами:

1) если в корреляционной матрице факторных переменных присутствуют коэффициенты парной корреляции по абсолютной величине большие 0,8, то делают вывод, что в данной модели множественной регрессии существует мультиколлинеарность;

2) вычисляют собственные числа корреляционной матрицы факторных переменных λmin и λ max . Если λ min‹10-5 , то в модели регрессии присутствует мультиколлинеарность. Если отношение

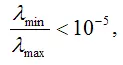
то также делают вывод о наличии мультиколлинеарных факторных переменных;

3) вычисляют определитель корреляционной матрицы факторных переменных. Если его величина очень мала, то в модели регрессии присутствует мультиколлинеарность.

Если оцененную модель регрессии предполагается использовать для изучения экономических связей, то устранение мультиколлинеарных факторов является обязательным, потому что их наличие в модели может привести к неправильным знакам коэффициентов регрессии.

При построении прогноза на основе модели регрессии с мультиколлинеарными факторами необходимо оценивать ситуацию по величине ошибки прогноза. Если её величина является удовлетворительной, то модель можно использовать, несмотря на мультиколлинеарность. Если же величина ошибки прогноза большая, то устранение мультиколлинеарных факторов из модели регрессии является одним из методов повышения точности прогноза.

К основным способам устранения мультиколлинеарности в модели множественной регрессии относятся:

1) один из наиболее простых способов устранения мультиколлинеарности состоит в получении дополнительных данных. Однако на практике в некоторых случаях реализация данного метода может быть весьма затруднительна;

2) способ преобразования переменных, например, вместо значений всех переменных, участвующих в модели (и результативной в том числе) можно взять их логарифмы:

lny=β0+β1lnx1+β2lnx2+ε .

Однако данный способ также не способен гарантировать полного устранения мультиколлинеарности факторов;

Если рассмотренные способы не помогли устранить мультиколлинеарность факторов, то переходят к использованию смещённых методов оценки неизвестных параметров модели регрессии, или методов исключения переменных из модели множественной регрессии.

Если ни одну из факторных переменных, включённых в модель множественной регрессии, исключить нельзя, то применяют один из основных смещённых методов оценки коэффициентов модели регрессии – гребневую регрессиюили ридж(ridge).

При использовании метода гребневой регрессии ко всем диагональным элементам матрицы ( ХТХ ) добавляется небольшое число τ : 10-6 ‹ τ ‹ 0.1. Оценивание неизвестных параметров модели множественной регрессии осуществляется по формуле:

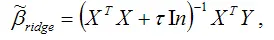
где ln – единичная матрица.

Результатом применения гребневой регрессии является уменьшение стандартных ошибок коэффициентов модели множественной регрессии по причине их стабилизации к определённому числу.

Метод главных компонент является одним из основных методов исключения переменных из модели множественной регрессии.

Данный метод используется для исключения или уменьшения мультиколлинеарности факторных переменных модели регрессии. Суть метода заключается в сокращении числа факторных переменных до наиболее существенно влияющих факторов. Это достигается с помощью линейного преобразования всех факторных переменных xi (i=0,…,n) в новые переменные, называемые главными компонентами, т. е. осуществляется переход от матрицы факторных переменных Х к матрице главных компонент F . При этом выдвигается требование, чтобы выделению первой главной компоненты соответствовал максимум общей дисперсии всех факторных переменных xi (i=0,…,n), второй компоненте – максимум оставшейся дисперсии, после того как влияние первой главной компоненты исключается и т. д.

Метод пошагового включенияпеременных состоит в выборе из всего возможного набора факторных переменных именно те, которые оказывают существенное влияние на результативную переменную.

Метод пошагового включения осуществляется по следующему алгоритму: