Ангелина Яковлева - Ответы на экзаменационные билеты по эконометрике

Критическое значение t-критерия tкрит(а,N–1) определяется по таблице распределения Стьюдента, где а – уровень значимости, ( N-1 ) – число степеней свободы.

Наблюдаемое значение t-критерия при проверке основной гипотезы определяется по формуле:

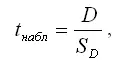
где SD – стандартное отклонение величины D . Значения SD для временных рядов, длиной от 10 до 100 наблюдений, занесены в специальную таблицу.

При проверке гипотез возможны следующие ситуации.

Если наблюдаемое значение t-критерия (вычисленное по выборочным данным) по модулю больше критического значения t-критерия (определённого по таблице распределения Стьюдента), т. е. |tнабл|>tкрит , то основная гипотеза отвергается. Следовательно, в исходном временном ряду присутствует трендовая компонента.

Если наблюдаемое значение t-критерия (вычисленное по выборочным данным) по модулю меньше или равно критического значения t-критерия (определённого по таблице распределения Стьюдента), т.е. |tнабл|≤tкрит , то основная гипотеза принимается. Следовательно, в исходном временном ряду отсутствует трендовая компонента.

С помощью метода или теста Чоу проверяется основная гипотеза о стабильности временного ряда. Если ряд характеризуется нестабильной тенденцией, то с определённого момента времени t* происходит изменение характера динамики анализируемого показателя под влиянием ряда внешних факторов, что в результате приводит к изменению параметров уравнения тренда, описывающего данную динамику.

Следовательно, весь временной ряд можно разделить на две подвыборки: первая подвыборка содержит значения временного ряда до переломного момента t* и вторая подвыборка содержит значения временного ряда после переломного момента.

Будем считать, что весь временной ряд представляет собой модель регрессии модель без ограничений. Обозначим данную модель через UN . Отдельными подвыборками будем считать частные случаи модели регрессии без ограничений. Обозначим эти частные подвыборки как PR .

Введём следующие обозначения:

PR1 – первая подвыборка;

PR2 – вторая подвыборка;

ESS(PR1) – сумма квадратов остатков для первой подвыборки;

ESS(PR2) – сумма квадратов остатков для второй подвыборки;

ESS(UN) – сумма квадратов остатков для общей модели регрессии.

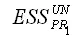
– сумма квадратов остатков для наблюдений первой подвыборки в общей модели регрессии;

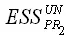
– сумма квадратов остатков для наблюдений второй подвыборки в общей модели регрессии.

Для частных моделей регрессии справедливы следующие неравенства:

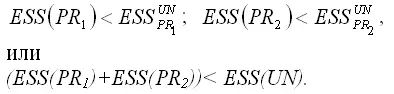
Условие (ESS(PR1)+ESS(PR2))= ESS(UN) выполняется только в том случае, если коэффициенты частных моделей регрессии и коэффициенты общей модели регрессии без ограничений будут одинаковы, но на практике такое совпадение встречается очень редко.

Основная гипотеза формулируется как утверждение о структурной стабильности тенденции общего временного ряда.

Альтернативная или обратная гипотеза формулируется как утверждение о структурной нестабильности тенденции общего временного ряда

Данные гипотезы проверяются с помощью F-критерия Фишера-Снедекора.

Наблюдаемое значение F-критерия сравнивают с критическим значением F-критерия, которое определяется по таблице распределения Фишера-Снедекора.

Критическое значение F-критерия Фишера определяется по таблице распределения Фишера-Снедекора в зависимости от уровня значимости а и двух степеней свободы k1=m+1 и k2=n-2m-2.

Наблюдаемое значение F-критерия рассчитывается по формуле:

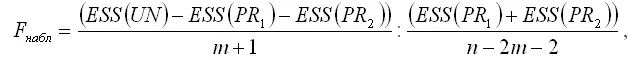
где ESS(UN) – ESS(PR1) – ESS(PR2) – величина, характеризующая улучшение качества модели регрессии после разделения её на подвыборки;

m – количество факторных переменных (в том числе фиктивных);

n – объём общей выборочной совокупности.

При проверке выдвинутых гипотез возможны следующие ситуации.

Если наблюдаемое значение F-критерия (вычисленное по выборочным данным) больше критического значения F-критерия (определённого по таблице распределения Фишера-Снедекора), т. е. Fнабл≥Fкрит , то основная гипотеза отклоняется. Следовательно, исходный временной ряд не имеет общей стабильной тенденции.

Если наблюдаемое значение F-критерия (вычисленное по выборочным данным) меньше или равно критического значения F-критерия (определённого по таблице распределения Фишера-Снедекора), т. е. Fнабл‹Fкрит , то основная гипотеза принимается. Следовательно, исходный временной ряд может быть описан одним трендовым уравнением.

Метод аналитического выравнивания с помощью функций времени или кривых роста является основным методом представления тренда в аналитическом виде, используемым в эконометрике. Суть данного метода заключается в аппроксимации временного ряда определённой формой регрессионной кривой. При этом наиболее проблематичным является вопрос о выборе функции тренда.

Выбор выравнивающей кривой может осуществляться на основании заранее заданных критериев, к которым относятся:

1) множественный коэффициент детерминации;

2) сумма квадратов отклонений наблюдаемых значений временного ряда от теоретических значений (рассчитанных с помощью функции тренда).

Методом конечных разностейназывается метод, позволяющий подобрать подходящую форму кривой. Его применение возможно в том случае, если временной ряд содержит равностоящие друг от друга уровни.

Конечной разностью первого порядка(разностным оператором первого порядка) называется разность между соседними уровнями временного ряда:

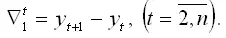
Разностным оператором второго порядка(конечной разностью второго порядка) называется разность между соседними разностными операторами первого порядка:

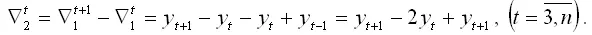
В общем случае разностным оператором i-го порядканазывается разность между соседними разностными операторами (i-1)-го порядка: