Ангелина Яковлева - Ответы на экзаменационные билеты по эконометрике

В дополнение к выборочным коэффициентам асимметрии и эксцесса рассчитывают показатели среднеквадратических отклонений данных коэффициентов по формулам:

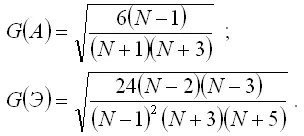
Если одновременно выполняются следующие неравенства:

1) |КА|≤1,5G(A);

2) |КЭ|≤1,5G(Э),

то гипотеза о нормальном характере распределения случайной компоненты принимается. Если хотя бы одно из указанных неравенств нарушается, то гипотеза о нормальном распределении остатков отвергается.

Помимо адекватности выбранной модели, необходимо охарактеризовать её точность. Наиболее простым критерием точности модели является относительная ошибка, рассчитываемая по формуле:

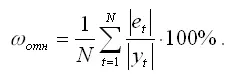
Если относительная ошибка равна менее, чем 13 %, то точность подобранной модели признаётся удовлетворительной.

Для построения адекватной модели временного ряда необходимо охарактеризовать сезонные и циклические компоненты временного ряда. К основным методам моделирования сезонных и циклических колебаний относятся:

1) метод вычисления сезонной компоненты и построение аддитивной или мультипликативной модели временного ряда;

2) метод применения сезонных фиктивных переменных;

3) метод анализа сезонных колебаний с помощью автокорреляционной функции;

4) метод, основанный на использовании одномерных рядов Фурье.

В связи с тем, что моделирование сезонных и циклических колебаний происходит аналогично, применение данных методов мы будем рассматривать на примере моделирования сезонных колебаний.

Аддитивная модель временного ряда стоится в том случае, если амплитуда сезонных колебаний не меняется во времени:

yt=Tt+St+εt,

где T – это трендовая компонента;

S – это сезонная компонента;

ε – случайный шум.

Мультипликативная модель временного ряда стоится в том случае, если амплитуда сезонных колебаний изменяется во времени:

yt=Tt*St+εt.

Предположим, что задача состоит в исследовании временного ряда Xij , где i – это номер сезона (периода времени внутри года, например, месяца или квартала),

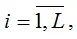
L – число сезонов в году, j – номер года,

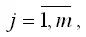
m – общее количество лет. Количество уровней исходного временного ряда равно n=L*m .

Прежде чем рассчитывать сезонную компоненту, исходный временной ряд необходимо выровнять. Для этого применяются методы механического выравнивания, к которым относятся:

1) метод скользящих средних;

2) метод экспоненциального сглаживания;

3) метод медианного сглаживания и др.

Результатом процедуры сглаживания будет временной ряд выровненных значений

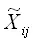
не содержащих сезонной компоненты.

Если временной ряд представлен аддитивной моделью, то в качестве сезонной компоненты используется показатель абсолютного отклонения – Sai . Сумма всех сезонных компонент, т.е. показателей абсолютных отклонений Sai . должна быть равна нулю.

Если временной ряд представлен мультипликативной моделью, то в качестве сезонной компоненты используется индекс сезонности – Isi . Произведение всех сезонных компонент, т. е. индексов сезонности Isi , должно быть равно единице.

Показатель абсолютного отклонения в i-том сезоне рассчитывается как среднее арифметическое из отклонений фактического и выровненного уровней временного ряда:

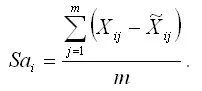
Индекс сезонности в i-том сезоне рассчитывается как среднее арифметическое из отношений фактического уровня временного ряда к выровненному:

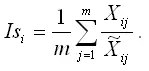
Если при построении аддитивной модели временного ряда сумма всех абсолютных отклонений не равна нулю, то рассчитываются скорректированные значения сезонных компонент по формуле:

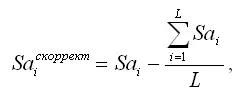
где L – общее количество сезонных компонент.

На следующем этапе построения модели временного ряда осуществляется расчёт трендовой компоненты с помощью метода аналитического выравнивания функциями времени или кривыми роста. Данный метод выравнивания применяют не к исходному временному ряду, а к временному ряду с исключённой сезонной компонентой. При этом уровни исходного временного ряда корректируются на величину сезонной компоненты следующим образом:

1) для аддитивной модели из исходных уровней вычитаются показатели абсолютных отклонений Sai ;

2) для мультипликативной модели уровни исходного временного ряда делятся на индексы сезонности Isi .

Метод сезонных фиктивных переменных относится к методам моделирования сезонных компонент временного ряда. Суть данного метода заключается в построении модели регрессии, которая наряду с фактором времени включает сезонные фиктивные переменные.

Фиктивной переменной(dummy variable) называется атрибутивный или качественный фактор, представленный с помощью определённого цифрового кода.

Моделью регрессии с переменной структуройназывается модель регрессии, включающая в качестве факторной (факторных) переменных фиктивную переменную.

Предположим, что задача состоит в исследовании временного ряда Xij , где i – это номер сезона (периода времени внутри года, например, месяца или квартала),

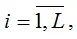
L – число сезонов в году, j – номер года,

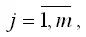
m – общее количество лет. Количество уровней исходного временного ряда равно n=L*m .

При построении модели регрессии с переменной структурой необходимо учитывать, что число сезонных фиктивных переменных всегда должно быть на единицу меньше сезонов внутри года, т. е. должно быть равно величине L-1 . Например, при моделировании годовых данных модель регрессии помимо фактора времени должна содержать одиннадцать фиктивных компонент (12-1). При моделировании поквартальных данных модель регрессии должна содержать три фиктивные компоненты (4-1) и т. д.