Айван Пастин - Теория игр в комиксах

Исследование группового поведения представляет некоторую трудность для теории игр, так как группа как целое может казаться иррациональной, даже если каждый член этой группы рационален.

У рациональных людей, принимающих решения, переходные предпочтения. Это значит, что если он предпочитает альтернативу А альтернативе Б и предпочитает альтернативу Б альтернативе В, то он должен будет предпочесть альтернативу А альтернативе В (символ «>» означает «предпочтительнее»):

А > Б и Б > В, значит, А > В

Тем не менее, когда все члены группы рациональны, групповые предпочтения могут быть непереходными.

То есть для групп А > Б и Б > В не обязательно означает, что А > В.

Мы можем наблюдать непереходные групповые предпочтения в действии в примере с городом, во владении которого находится свободный участок земли. Существует три возможных варианта действий. На нем можно разбить парк, построить центр по переработке мусора или школу.

Городской совет должен решить судьбу этого земельного участка. В совете три человека. Каждый член совета имеет свой первый выбор.

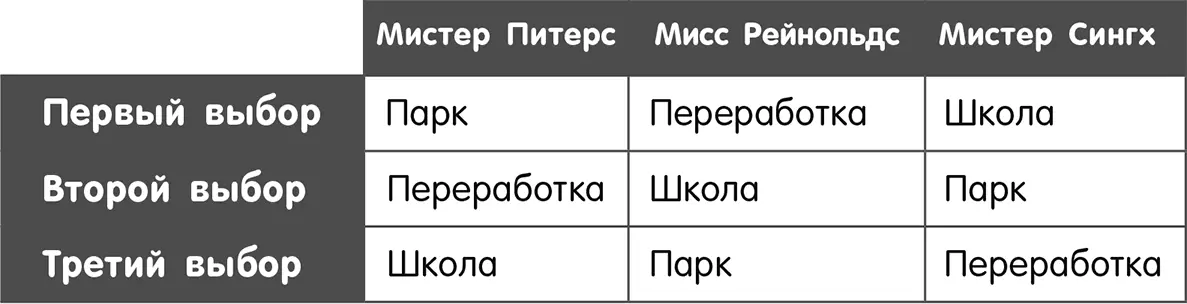
Совет проводит голосование, теперь они решают между двумя вариантами за один раз. Предположим, что каждый член совета голосует за вариант, который он действительно предпочитает, то есть мы наблюдаем искреннее голосование.

Двое проголосовали за школу, один – за парк. Как группа они предпочитают школу парку, значит, они точно не будут разбивать парк:

Школа > Парк

Остается лишь выбрать между центром по переработке мусора и школой.

За постройку центра по переработке мусора проголосовали двое, а за школу один член совета:

Центр по переработке мусора > Школа

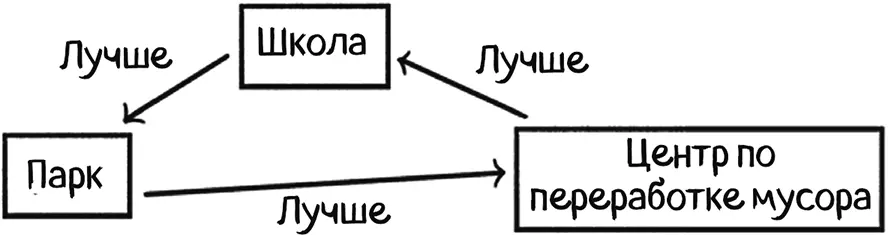
Значит, решено. Совет решил, что школа лучше парка, а центр по переработке мусора лучше школы.

В ходе выбора между центром по переработке мусора и парком мистер Питерс голосовал за парк (его первый выбор), мисс Рейнольдс – за центр (ее первый выбор), а мистер Сингх – за парк, так как центр был для него худшим выбором. Совет решил, что парк лучше центра по переработке мусора (два голоса против одного):

Парк > Центр по переработке мусора

Каждый член совета имеет переходные предпочтения и голосует искренне. Однако при совместных действиях предпочтения совета становятся непереходными, то есть вне зависимости от итогового выбора группы члены группы всегда будут считать, что другой вариант лучше.

Американский экономист Кеннет Эрроу(род. в 1921 г.) в 1972 году был награжден Нобелевской премией по экономике за его теорему невозможности Эрроу. Согласно ей, в группах, которыми не управляет диктатор, всегда будет вероятность того, что предпочтения станут непереходными, при которых мы будем отвергать выбор, который мог бы быть оптимален для всех, или при которых незначительные детали влияют на наш выбор. Этих проблем не избежать при групповом принятии решений.

Теорема невозможности Эрроу объясняет, почему люди на совещаниях комитетов и на парламентских собраниях часто ведут себя так странно. К примеру, на комитетских совещаниях члены комитета часто поднимают одну и ту же тему.

Существует много способов организовать групповое принятие решений. Возможна как автократия, при которой один человек принимает все решения в зависимости от его предпочтений, так и классическая демократия, при которой все члены групп обладают правом голоса при принятии решения. Помимо этих крайностей имеются и другие возможные системы.

В теореме невозможности Эрроу доказывается, что при любой системе, кроме автократии, в процессе принятия групповых решений всегда будет сохраняться вероятность непоследовательного поведения группы.

Теорию игр начали воспринимать как самостоятельный научный метод в 1940-х годах, однако ее центральные вопросы взаимодействия и конфликта стары как мир.

К примеру, английский философ Томас Гоббс(1588–1679) в своем произведении «Левиафан» пишет:

Его утверждение по природе своей гармонично со всей теорией игр: без сильного правительства, которое бы способствовало заключению соглашений, кооперация провалилась бы, потому что каждый игрок волновался бы об аморальности соперника, что также привело бы к жестокости.

Примеры размышлений в духе теории игр можно найти еще в текстах Платона, который передавал воспоминание Сократа о битве при Делии (424 г. до н. э.).

Развитие теории игр как научной дисциплины предоставило нам возможность в мельчайших деталях исследовать конфликт и кооперацию.

Теперь мы можем ответить на вопросы, на которые было почти невозможно дать ответ раньше.

Из-за математической основы и способов представления большинства явлений теории игр новичкам бывает сложно разобраться в сути и овладеть необходимым инструментарием. Поэтому в настоящей книге мы старательно избегали усложнения и концентрировались на основных идеях теории игр.