Айван Пастин - Теория игр в комиксах

Если особей с поведением «ястреба» в популяции больше ⅚ (то есть, если р > ⅚), то «голуби» будут выживать и размножаться в больших количествах, чем «ястребы», так что часть популяции, запрограммированная на поведение «ястребов», (р) уменьшится.

В долгосрочной перспективе силы эволюции спровоцируют изменение в количестве особей каждого типа. Численность «ястребов» будет стремиться к ⅚ от всей популяции, а «голубей» – к ⅙. Мы имеем дело с такими точными пропорциями благодаря числам, которые мы указывали в платежной матрице. Однако как только цена конфликта станет выше ценности желанной добычи, эволюционные силы внесут свои коррективы в популяцию и заставят «голубей» и «ястребов» сосуществовать.

В долгосрочной перспективе «ястребы» и «голуби» будут сосуществовать в рамках одной популяции в соотношении 5 к 1, при этом оба вида в среднем будут нормально функционировать. При столкновении с «голубями» «ястребы» будут присваивать все ресурсы, но возможность серьезных увечий для них будет очень высока при схватке с другими «ястребами». «Голуби» не смогут удержать ресурсы, когда окажутся в паре с «ястребами», но никогда не пострадают в бою.

Такое долгосрочное эволюционное «устойчивое состояние», при котором количество «ястребов» в популяции равно ⅚, называется эволюционно стабильным равновесием. Это такое равновесие, которое сохраняет свою стабильность, даже если мы добавляем к одной группе животных некое количество особей, запрограммированных по-другому, в силу того, что эволюционные силы рано или поздно восстанавливают равновесие.

Вообще в эволюционных играх может быть множество исходов. В «Ястребах и голубях» наблюдается единственное эволюционно стабильное равновесие, а долгосрочное устойчивое состояние рано или поздно будет восстановлено, вне зависимости от того, сколько запрограммированных по-другому особей мы добавим.

Однако в некоторых играх возможно более чем одно эволюционно стабильное равновесие. В таких играх силы эволюции восстановят пропорции равновесия, если наблюдаются незначительные изменения в популяции. Но крупные изменения в составе популяции могут повлечь за собой совсем иное равновесие.

Некоторые игры вообще не имеют эволюционно стабильного равновесия. В таких играх популяция никогда не добьется стабильного устойчивого состояния. Наоборот, она окажется под влиянием цикличных изменений, при которых группы различных видов животных будут бесконечно то увеличиваться, то уменьшаться.

Интересно то, что эволюционно стабильное соотношение «ястребов» к остальной популяции (⅚) также было бы равно равновесной вероятности в равновесии Нэша в смешанных стратегиях, если бы животные выбирали стратегии рационально. И это не совпадение. Чтобы рассчитать равновесные вероятности в равновесии Нэша в смешанных стратегиях, мы должны найти такие вероятности, при которых игрокам безразлично, что выбрать – линию поведения «ястреба» или «голубя». В равновесии ожидаемые ценности обеих стратегий равны.

В «Ястребах и голубях» мы имеем дело с таким же уровнем ожидаемой эволюционной приспособленности обоих видов животных в эволюционно стабильных равновесных соотношениях. Если бы их приспособленность различалась, силам эволюции пришлось бы выделить один вид животных, существование которого было бы намного более благоприятным, чем у другого, вплоть до момента, когда было бы достигнуто устойчивое состояние.

В «Ястребах и голубях» эволюционно стабильное равновесие создает соотношение «ястребов» и «голубей» в рамках популяции, что похоже на интерпретацию равновесия Нэша в смешанных стратегиях в игре «Уклонение от уплаты налогов». В том случае равновесие создавало соотношение уклонистов и законопослушных налогоплательщиков, а решения, которые принимали игроки, были рациональными.

Когда речь идет об эволюции, концентрация на эволюционно стабильном равновесии разумна, так как она позволяет исключить равновесие, которое не выдержало бы и малейших изменений в популяции.

Часто так случается, что игроки могут проследить действия своих оппонентов перед принятием собственного решения. В некоторых играх существует порядок, в котором участники делают ходы. Они называются играми с последовательными ходами. В большинстве настольных игр, вроде шахмат, игроки совершают ходы последовательно, один за другим.

К примеру, предприниматель размышляет, стоит ей открывать кафе на определенном перекрестке или нет. При этом она может учитывать, какие магазины уже открыты поблизости, а также попробует предугадать, какие еще магазины появятся там в будущем, если она все-таки откроет там кафе.

Игры с последовательными ходами динамичны, то есть игроки могут принимать свои решения, базируясь на изучении предыдущих действий соперников и на ожиданиях их будущих действий. Участники пытаются предугадать, что их оппоненты предпримут в ответ на их возможные действия, и затем, разворачивая эту цепочку с конца, принимают решение.

Мы можем рассмотреть трудности, которые возникают в играх с последовательными ходами, с помощью динамичной версии игры с одновременными ходами. Тут нам пригодится «Битва полов».

В обычной «Битве полов» Боб и Эми должны принять решение о планах на вечер поодиночке и одновременно. Они хотят провести вечер вместе, но им нравятся разные занятия. Помните стратегическую форму первой «Битвы полов»?

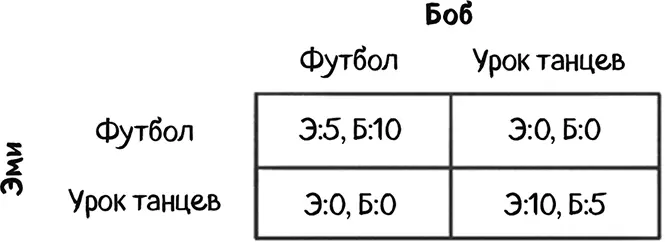
А теперь давайте немного изменим их историю. Предположим, что рабочий день Эми заканчивается на час раньше рабочего дня Боба. Она идет к месту проведения одного из занятий и звонит Бобу, чтобы сообщить, где находится. Как только она позвонила ему, у нее больше нет возможности поменять свое местоположение, но Боб пока может пойти на стадион или в танцевальный класс.