Роланд Глазер - Биология в новом свете

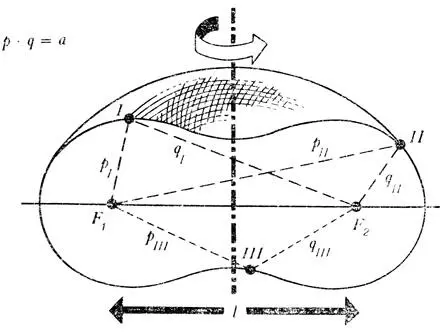
Кривая Кассини — геометрическое место точек, для которых произведение расстояний до двух заданных точек F 1 и F 2 есть постоянная величина. С помощью этой кривой можно описать форму эритроцитов

Таким образом, форму кровяных клеток человека можно охарактеризовать двумя величинами, а именно константой a и расстоянием между точками F 1и F 2, обозначенным буквой l. Как только отношение а к l изменится, изменится и форма кривой; следовательно, разбухание клеток можно моделировать изменением этого отношения.

Теперь, основываясь на соответствующих физических законах, можно рассчитать энергию, необходимую для деформации эластичной клеточной мембраны при заданных объеме и поверхности клетки. Расчет весьма сложен, но вычислительная машина способна выполнить его с достаточной точностью. В результате мы получим связь между энергией и фактором формы, равным отношению a/l. На рисунке показано, что такую связь, такой функционал можно изобразить в виде кривой, которая имеет один минимум. В точке минимума на деформацию эластичной клеточной мембраны затрачивается наименьшее количество энергии. Как мы видим, в этой точке фактор формы принимает именно такое значение, при котором кривая Кассини соответствует форме эритроцита. Итак, форма наших эритроцитов оптимальна; теперь мы знаем, какие процессы оптимизируются, и в состоянии правильно понять нарушения, связанные с изменением формы эритроцитов у больных. Это может быть одним из путей, ведущих к устранению причин болезни.

Однако подобный анализ объясняет проблему лишь частично. Мы говорили об энергии деформации, обусловленной молекулярным строением клеточной мембраны — пленки толщиной около 1/100 000 мм, окружающей клетку. Для полноты картины следовало бы взглянуть на данную проблему и с позиций молекулярной биофизики, но это увело бы нас далеко от основной темы. Вопросами молекулярной биофизики мы займемся в конце книги. А сейчас вернемся к теме о форме живых организмов в системе координат. Мы видели, что эту форму можно описать математически, т. е. представить в виде чисел и кривых. Более того, с помощью математических выкладок и с учетом физических закономерностей мы можем рассчитать ее изменение, развитие, приспособленность, или, говоря математическим языком, оптимальность. Пример с эритроцитами человека сравнительно прост. Он прост настолько, что хорошая ЭВМ в состоянии его исчерпывающе обсчитать. В большинстве других случаев формы организмов много сложнее и подобные расчеты чрезвычайно затруднительны. Тем не менее такие случаи стоит рассмотреть хотя бы потому, что они позволяют выявить некоторые общие интересные закономерности.

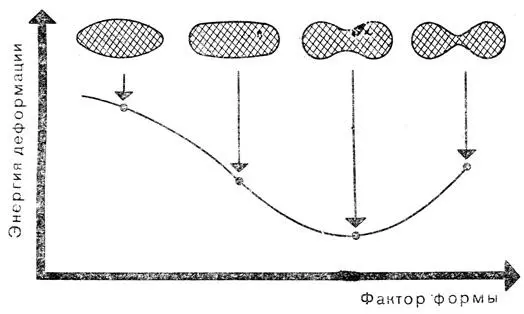
Эритроцит имеет такую форму, которая при заданных поверхности и объеме клетки соответствует минимальной энергии деформации оболочки. Расчет зависимости между формой и энергией в данном случае достаточно сложен, однако принципиально он не отличается от расчета оптимальной формы сада

Внешний вид растения, например, можно описать шестью уравнениями, которые отражают как физические условия стабильности, так и законы синтеза и транспорта веществ. С уравнениями такого рода мы уже встречались в первой главе. Если стебель будет слишком высоким, он сломается. То же можно сказать о ветвях, черенках листьев и т. п. С другой стороны, чём длиннее ветви, тем больше поверхность листвы, освещаемая солнцем. Листья обеспечиваются водой, идущей от корней; прежде чем испариться вода должна достигнуть самых удаленных веточек. Каждое из этих требований можно выразить в виде уравнений. Оптимальное решение этих уравнений определяет вид растения. Каков он? Существует одно оптимальное решение или их может быть несколько?

Оптимизация возможна по многим факторам. Вспомним хотя бы пример с постройкой моста. Мост должен быть наиболее дешевым, надежным и легким. Растение тоже стремится к оптимуму по засухоустойчивости, высоте, сопротивляемости ветру, что позволяет ему одержать верх над другими растениями в борьбе за свет. При определенных условиях один из этих факторов может приобрести решающее значение, и тогда оптимизация пойдет по нему; так, кактус обладает оптимальной защитой от засухи, а деревья оптимально используют поверхность листьев. Поэтому и существует не одна форма растений, которая является "особенно" оптимальной, а огромное разнообразие окружающего нас растительного мира.

Расчет кривой развития биологического вида путем решения дифференциального уравнения дает бесконечное множество кривых, и только выбор начала отсчета а 0 отводит одной из кривых роль 'частного решения'. Если в некоторых 'критических' точках кривые расходятся, это означает, что родословная разветвляется. По осям отложены произвольно выбранные параметры организмов a и b

Остановимся на растениях и попытаемся разобраться в некоторых особенностях их эволюции с точки зрения теории оптимальных процессов. Сущность оптимизации состоит в приспособлении вида к окружающей среде. Как мы уже знаем, развитие формы растений можно проанализировать путем решения задачи по оптимизации, представляя процесс развития в виде математического уравнения. Такого рода уравнения называются дифференциальными. В следующей главе мы рассмотрим математическое описание биологических процессов подробнее, а сейчас отметим лишь, что решением дифференциального уравнения является целое семейство кривых, а не одно или несколько числовых значений.

Итак, мы получим множество кривых развития, различающихся между собой по форме и направлению. И только решив, какую точку на плоскости считать за исходную, мы сможем отбросить все кривые, не проходящие через эту точку, и оставить одну, которая и является действительным, или, как говорят, частным", решением нашей задачи. Следовательно, эволюция нашего растения должна идти вдоль этой кривой в направлении оптимума.

Не исключено, что одна из отброшенных нами кривых в какой-то точке сближается с действительной кривой, а потом они снова расходятся. В такой точке процесс эволюции не стабилен. Путем мелких, случайных изменений, иначе говоря, мутаций, индивидуум как бы совершает "прыжок в сторону". Он переходит на "боковую колею" и движется уже по другому пути. Процесс эволюции как бы "раздваивается".