Роланд Глазер - Биология в новом свете

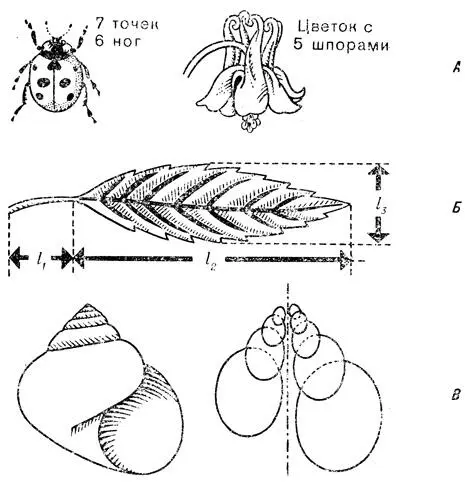
Числа (А), размеры (Б) и математические функции (В) — основа для точного сопоставления биологических форм

Почему мы выбрали именно эти два параметра? Может быть, они наиболее характерны? Ничего подобного! С таким же успехом мы могли бы взять число листьев в розетке, длину листьев, диаметр головки соцветия и т. д. После того как нам удалось свести два параметра к одной точке, многообразие живой природы снова озадачивает нас, Если к двум параметрам добавить третий, то для каждой конкретной маргаритки мы получим точку уже не на плоскости, а в пространстве, и для всех маргариток, растущих на этом лугу, — объемное облако точек, которое характеризует целый вид. А что дальше?

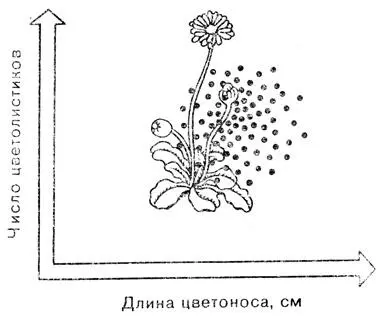
Выбранные параметры маргаритки отложены по осям системы координат. В результате измерений этих параметров для различных растений исследуемого вида мы получаем в фазовом пространстве облачко точек, характерное для данного вида. Каждому из растений соответствует одна точка в этом облачке

Такой вопрос может возникнуть только у человека, далекого от математики, который убежден в том, что все существующее можно представить зрительно. Математик думает иначе, он живет в мире абстрактного. Если трех измерений не хватает, то пусть будет 4, 5, 6, 10 или, наконец, n измерений, то есть сколь угодно много. И хотя с каждым новым измерением расчеты усложняются, в принципе можно рассчитать любое многомерное пространство. Но теперь слово "пространство" обозначает нечто совершенно отличное от того, что мы обычно изображаем в виде трехмерной структуры. Многомерные пространства используют в своих расчетах также физики-теоретики и называют их фазовыми пространствами. У нас нет причин искать какое-либо другое название. Итак, биологический вид есть облако точек в n-мерном фазовом пространстве.

Математическое обоснование тривиального — что это? Опять игра? Отнюдь нет! То, чем мы здесь занимаемся, относится к области бурно развивающейся сейчас нумерической таксономии. Облако точек вытягивается в длину и разделяется — возникает новый вид. Облако плывет — вид изменяется. Облака находятся близко или далеко друг от друга — это характеризует степень родства различных видов. В принципе все эти процессы можно рассчитать. Но здесь не обойтись, конечно, без быстродействующих электронных вычислительных машин.

Измерение плюс вычисление — это только один из возможных путей, ведущих к пониманию формы живого. Сколько нужно цифр чтобы правильно отобразить форму листа, контуры лягушки или панцирь рака? Конечно, с помощью числового метода мы можем охарактеризовать эти формы с большей или меньшей точностью, в зависимости от числа измеряемых параметров. Но это недостойно истинного математика; к тому же каждое новое измерение увеличивает степень многомерности фазового пространства, что делает расчеты неоправданно сложными. Значительно удобнее выявлять формы не по цифрам, а по аналогии. Это значит, что мы ищем математическую кривую, которая соответствует интересующей нас форме, т. е. аналогична ей, и может быть выражена формулой с возможно меньшим количеством постоянных величин, или констант.

Математикам известна такая универсальная формула, или, точнее, функция, которая позволяет математически выразить почти любую кривую, — это так называемый полином. Он записывается в виде ряда, который можно продолжать сколь угодно долго, но математик ограничивается лишь действительно необходимым числом членов, ибо с каждым новым членом полином все усложняется. Уравнение этого ряда выглядит так:

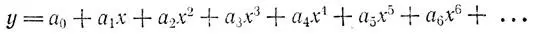
Оно показывает, как изменяется величина у в зависимости от изменения независимо меняющейся величины x . Обычно говорят, что y есть функция от x . Если значения x и у откладывать по осям системы координат, то мы получим кривую. Буквы a 0, a 1, a 2, a 3, a 4, a 5, a 6,... обозначают константы, они могут быть положительными и отрицательными, большими, малыми и даже равными нулю. Меняя значения этих констант, математик "изгибает" кривую до тех пор, пока она не примет желаемую форму. Для описания простых кривых достаточно ограничиться малым количеством членов такого полинома. Сколько нужно сделать отдельных измерений, чтобы получить изображенный на рисунке полином четвертой степени, т. е. полином, содержащий член a 4 x 4? Чтобы записать точную формулу, требуется только пять значений, а именно константы a 0, a 1, a 2, a 3и a 4. Собственно говоря, можно даже обойтись без первого значения, т. е. положить a 0= 0, тогда ось симметрии листа будет скользить по оси абсцисс. Мы видим, что с каждым новым членом наш полином описывает форму листа несколько точнее. Таким образом, с помощью полинома мы можем описать формы любых объектов независимо от их размеров, а также сравнивать их между собой.

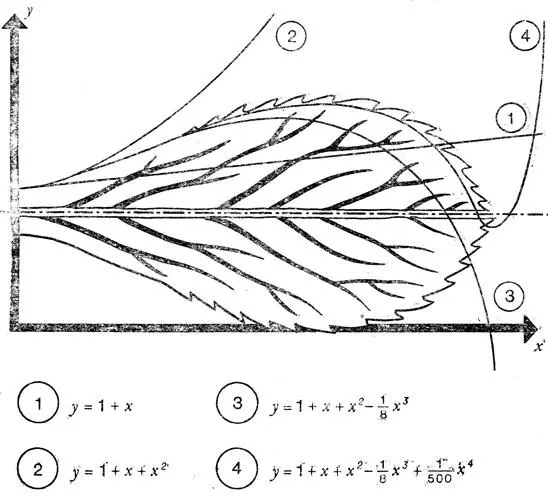
С помощью полинома, универсальной математической формулы, можно получить почти любую кривую. Чем сложнее кривая, тем большее число членов должен включать соответствующий полином. Можно попытаться подобрать полином, описывающий, например, форму листа

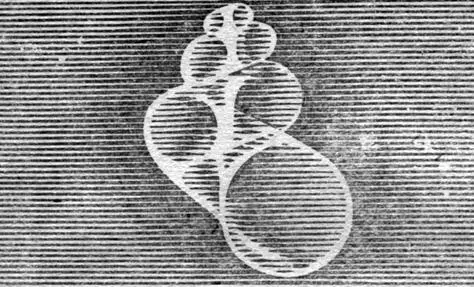
'Машинная улитка'. ЭВМ рассчитала форму улитки, которая лучше всего соответствует реальной

Если мы хотим получить замкнутую кривую, то есть представить лист целиком, то гораздо удобнее записать его форму в так называемых полярных координатах как функцию длины и угла вектора, поворачивающегося вокруг координатной оси.

На следующем рисунке показано, как можно с помощью ЭВМ обсчитать раковину улитки. Структуры аммонитов [3] Обширный отряд вымерших головоногих моллюсков; они обладали наружной раковиной, завитой в плоскую спираль с плотно налегающими оборотами. — Прим. ред. , так называемые лопастные, или шовные, линии, можно также выразить математически и соответствующие формулы ввести в память ЭВМ, что позволяет детально анализировать форму структур. Это имеет большое значение в палеонтологии и геологии, поскольку аммониты являются одной из самых важных групп "руководящих" ископаемых в некоторых слоях осадочных пород и по малейшим изменениям формы их лопастных линий можно судить о возрасте геологической породы.