Роланд Глазер - Биология в новом свете

Площадь S прямоугольника рассчитывается по формуле S = xy, где x и y — его стороны. Общую длину забора, т. е. периметр сада, обозначим l, тогда l = 2x + 2y, или х + у — l/2; у = l/2 — х. Заменив в формуле площади y этим выражением, получаем

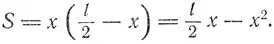
Эта формула позволяет рассчитать площадь S в зависимости от длины стороны x. Такую зависимость можно представить графически; соответствующая кривая показана на рисунке. Если сторона x очень мала, сторона y, согласно вышеприведенной формуле, должна приблизительно равняться. l/2. Сад превращается в узкое полотно с маленькой площадью. То же получается, когда x велико; x не может быть больше l/2, ибо в этом крайнем случае не хватило бы материала на другие стороны забора и сад состоял бы из двух параллельных заборов, не огораживающих никакой площади. Как подсказывает логика, кривая достигает максимума посередине, а именно в точке, где x принимает значение l/4. Легко подсчитать, что у также должен равняться l/4, следовательно, самую большую площадь имеет квадратный сад. Каждый студент знает, что положение максимума рассчитывается при помощи так называемой первой производной, в данном случае площади S по x. Эта математическая операция позволяет получить новое соотношение, характеризующее наклон функции S в каждой точке x : dS/dx = l/2 — 2x.

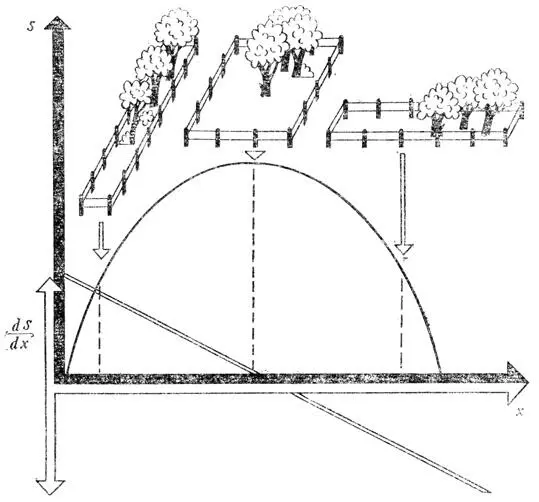
Парабола показывает, как изменяется площадь сада с заданной длиной забора l при изменении длины одной из сторон (например, x). Наклон этой параболы равен ее первой производной dS/dx (прямая линия). Точке пересечения прямой с осью x соответствует максимальное значение площади. Длина стороны x наибольшего по площади (квадратного) сада равна l/4

Максимум значения S находится в той точке, где наклон кривой равен нулю, т. е. dS/dx = 0. Подставив это значение в предыдущую формулу, получаем l/2 = 2x, или x = l/4. Не правда ли, легкая задача? А вообще говоря, это и есть задача по оптимизации. При заданной длине забора оптимизируется площадь сада.

В начале этой главы мы уже сформулировали типичную задачу по оптимизации. Каков самый короткий путь между двумя точками? Можно ли доказать математически, что это должна быть прямая или, может быть, существует какая-нибудь кривая, которая до сих пор ускользала от нашего внимания?

Здесь школьник уже встанет в тупик: ведь речь пойдет о максимальном или минимальном, т. е. в общем случае об оптимальном значении не какой-то величины, а целой функции. Как решать задачу на максимум-минимум для функции?

Выше мы говорили, что любую функцию, или кривую, можно представить в виде полинома с более или менее большим числом членов и затем охарактеризовать ее с помощью нескольких чисел, а именно констант a 0, a 1, a 2, … a n. В n — мерном фазовом пространстве такая кривая сводится к точке. Сдвиг точки означает изменение формы кривой, т. е. изменение вида функции.

Рассмотрим следующие уравнения:

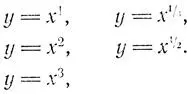
Здесь из полинома выбран только один член. Такое уравнение называют степенной функцией. В общем виде она записывается как у = x n, т. е. у равен x в n-й степени. С изменением значения n изменяется форма всей кривой.

Предположим, степенная функция описывает форму какого-нибудь биологического объекта и величина n связана с определенным свойством объекта подобно тому, как в предыдущей главе величина тела была связана с теплоотдачей. Этот случай напоминает задачу о длине забора для сада. Выяснив сначала математическую зависимость между величиной n и оптимизируемым свойством объекта, методами диференциального исчисления определяют максимум той математической функции, находят оптимальное значение n и, исходя из него, строят оптимальную кривую.

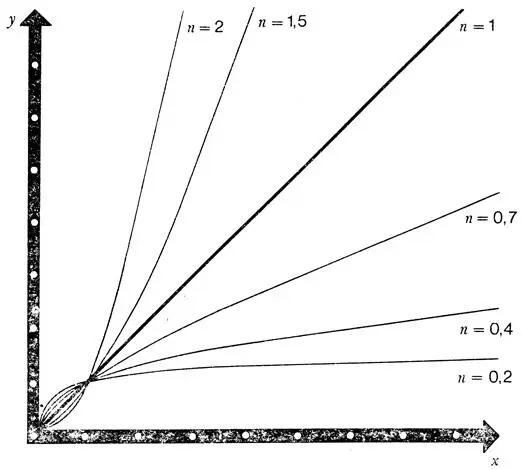
Семейство кривых у = x n . При изменении числа n изменяется форма кривой. Так эволюцию биологических форм в принципе можно представить, изменяя n

Однако здесь нам следует остановиться и подвести некоторые итоги. Математическая функция, описывающая какой-либо закон природы, отражает зависимость одной величины от другой и изображается формулой с характеристическими константами, т. е. числами, определяющими ее характер, изменение этих чисел влечет за собой изменение функции.

Характеристические константы могут быть связаны между собой с помощью другой математической функции, которая обусловливает первую функцию; это "суперфункция", или, как ее называют математики, функционал.

Таким образом, поиск оптимального решения сводится к отысканию функционала и определению его максимума (или минимума). Однако насколько просто описать этот процесс словами, настолько сложно выразить его математически, тем более что, как правило, для этого требуется проанализировать связь между многими изменяющимися величинами.

Рассмотрим конкретный пример. Красные кровяные клетки (эритроциты) человека имеют своеобразный вид. Они похожи на резиновые мячики, вдавленные с двух сторон. Для них такая форма оптимальна, потому что она обеспечивает быструю диффузию кислорода к гемоглобину — пигменту крови, содержащемуся в этих клетках. Но более интересна другая проблема, связанная с формой эритроцитов. В гипотонических растворах, т. е. растворах, содержащих меньше солей, чем кровь, кровяные клетки можно "надуть" — в них проникает вода, и они становятся округлыми. Если их осторожно перенести назад в изотонический раствор, восстанавливается прежняя двояковогнутая форма. Чем же она обусловлена? Почему на поверхности эритроцита не образуются другие вмятины? Вопрос интересен еще и потому, что при некоторых болезнях красные кровяные клетки действительно приобретают аномальную форму. Очевидно, нормальная форма красных кровяных клеток человека является следствием оптимального сочетания многих факторов.

Мы начнем анализ этой проблемы с того, что с помощью соответствующей математической формулы представим форму эритроцита в системе координат. Для этого, конечно, можно было бы найти подходящий полином, однако существует более изящный метод. Математикам известна некая кривая, являющаяся геометрическим местом точек, для которых произведение расстояний до двух заданных точек F 1и F 2есть величина постоянная. По имени получившего ее ученого она названа кривой Кассини. Итак, для каждой точки на кривой Кассини, изображенной на рисунке, должно быть справедливо уравнение p ⋅ q = а, где р и q — расстояния от этой точки на кривой до двух заданных точек F 1и F 2. Это уравнение, однако, описывает форму не всей клетки, а только ее поперечного сечения. Форма целой клетки получается вращением ее поперечного сечения вокруг центральной оси.