Роланд Глазер - Биология в новом свете

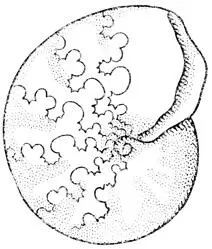
Лопастные линии в раковинах аммонитов. Эти кривые можно выразить математически и ввести в память ЭВМ

Итак, форму живого организма можно не только характеризовать размерам, но и описать математически.

Теперь попытаемся с помощью математических формул представить какой-нибудь биологический процесс, например выразить кривую роста. Уму непостижимо: сначала математическое описание формы, а теперь — биологического процесса! Но это кажется трудным только неспециалисту в силу инертности нашего повседневного мышления, привычки воспринимать лишь то, что мы непосредственно ощущаем органами чувств. Форму, то есть три измерения — длину, ширину и высоту, — мы "видим". А изменение этой формы, иначе говоря, изменение этих трех параметров во времени, мы "переживаем". Мы должны запастись терпением и временем и ждать. Для математика время, выраженное в секундах, часах, днях и т. д., такая же счетная величина, как длина и ширина. Если замысловатую форму растения мы выразили с помощью n параметров, представив ее точкой в n — мерном фазовом пространстве, то нам ничего не стоит добавить к ним (n + 1)-й параметр, время, и рассматривать изменение формы растения, т. е. его рост, как ход кривой в (n + 1)-мерном фазовом пространстве.

Итак, из звезды получается комета — звезда с хвостом, летящая по заранее определенному пути. Мы установили, что нумерическая таксономия позволяет представить биологический вид как облачко точек в фазовом пространстве. Если теперь мы добавим время, скажем, продолжительность жизни отдельной особи, то получим уже не облачко точек, а более или менее плотный пучок кривых, представляющих собой кривые роста. Несколько позже мы остановимся на них подробнее, а сейчас хотелось бы высказать еще одно соображение.

Ничто не в силах остановить математика. Не остановился он даже перед авторитетом Декарта, искривив прямоугольную систему координат, названную в честь величайшего математика и мыслителя XVII века "декартовой". Однако в качестве оправдания своих действий математик может сослаться на четвертое правило из "Рассуждений о методе" самого Декарта, которое гласит: "Для познания действительности необходим метод". И в данном случае метод состоит в том, что прямоугольную сетку линий вместе-с нанесенными на нее фигурами непрерывно изгибают в соответствии с формулами. На языке математики этот метод называется преобразованием системы координат.

Более пятидесяти лет назад д'Арси Томпсон написал книгу "Рост и форма" ( On Growth and Form, Cambridge , 1917). Это была одна из первых работ по математической биологии: в ней высказывалась мысль, что преобразование координат удобно применять для описания изменений биологических форм. На рисунке показан пример, приведенный в книге Томпсона, который отражает не рост отдельного организма, а видоизменение, превращение формы в процессе исторического развития. Томпсон пришел к следующему заключению: если рассматривать только внешнюю форму какого-либо организма и задать ее параметры в декартовой системе координат, то форму другого близкородственного организма можно считать результатом непрерывного изменения координат. Следовательно, процесс развития вида в целом можно описать математически соответствующим преобразованием системы координат.

Что это нам дает? Мы нашли способ отобразить природный процесс в формулах и числах. Эти числа вместе с программой мы можем ввести в ЭВМ, и машина с невероятной скоростью и "терпением" проведет самые сложные расчеты. ЭВМ сможет легко рассчитать все возможные промежуточные формы, независимо от того, существовали они или нет на ранних этапах истории Земли. Машина может также экстраполировать, т. е. "мысленно" продолжить путь эволюции. Нам же останется только решить, будет ли "рассчитанный" организм жизнеспособным в реальной действительности или нет. Однако все это справедливо лишь при условии, что с течением времени в соответствии с определенными правилами изменяются только формы, а сами правила, отражающие законы природы, остаются неизменными. Таким образом, буквально на глазах возникает новая проблема. К сожалению, мы не имеем возможности обсуждать ее здесь, хотя в последнее время она получила некоторое развитие.

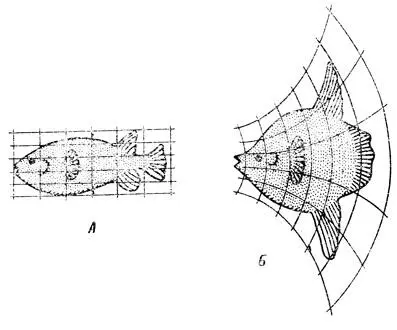
На примере формы тела у рыб близких родов [Diodon (А) и Qrthagoriscus (Б)] д' Арси Томпсон показал, что изменение формы можно описать с помощью соответствующего преобразования системы координат

Мы сделали первый шаг — заключили форму живого организма в систему координат, и не только форму, но и ее изменения. Как мы видели, это не просто, но тем не менее с помощью современной вычислительной техники можно добиться хороших результатов. Итак, в ЭВМ ввели параметры живого организма; она ждет приказа! Что с ними делать? Кое-что мы уже наметили. Машина должна, например, выяснить, насколько интересующий нас организм родствен какому-либо другому. Предположим, что получено число, которое соответствует расстоянию между двумя точками в фазовом пространстве и тем самым позволяет рассчитать степень родства двух организмов. ЭВМ должна установить, к какому виду, к какой расе и с какой вероятностью относится организм, форма которого характеризуется данными параметрами. Она должна высчитать, какую форму должен был бы иметь еще не открытый палеонтологами организм, который по своему геологическому возрасту, с одной стороны, старше, а с другой — моложе уже известных организмов. При этом может выясниться, что форма В произошла не от формы А, а возникла параллельно. Не так уж плохо! Однако в начале главы мы ставили перед собой более смелую задачу — найти ответ на вопрос: почему организм имеет ту или иную форму?

Вернемся к нашей исходной точке зрения, а именно к положению, что организм представляет собой систему, достигшую оптимальности в процессе борьбы за существование, и выясним, насколько применима здесь теория оптимальных процессов. В чем состоит суть этого метода? Это старая и в то же время новая отрасль математики. Старая, потому что данные методы возникли не сегодня, и новая — потому что внедрение и использование их на практике стало возможным только в век совершенных счетных машин. Началом теории оптимальных процессов можно считать формулу, которую свыше двухсот лет назад вывел великий математик Леонард Эйлер. Но предпосылки к созданию этой теории были заложены много раньше.

Излюбленной задачей в курсе дифференциального исчисления в вузах является следующая: "У хозяина есть материал для забора общей длиной l, которым он должен огородить прямоугольный сад со сторонами х и у. Рассчитать, при каком соотношении сторон площадь сада будет наибольшей". Решение этой задачи несложно.