Бен Орлин - Время переменных. Математический анализ в безумном мире

В эпической поэме Вергилия «Энеида» Элисса выступает как любовница титулованного Энея, основателя Рима. Вергилий называет ее Дидоной. Под этим именем она вошла в основной состав канона западной культуры: 11 раз ее упоминал Шекспир, она стала героиней 14 опер, а также появилась в компьютерной игре «Цивилизация». Как говорил Дидоне Эней, «твоя честь, твое имя, твои заслуги будут жить вечно».

В наши дни город Элиссы с периметром из бычьей шкуры является прибрежным пригородом Туниса.

Предупреждаю заранее: я собираюсь закончить эту главу длинной, укрепляющей серией обязательных упражнений. Вот такую книгу для чтения на пляже вы купили. Если только – здесь я просто немного подтруниваю – вы не обменяете эту домашнюю работу на книгу апокалиптических комиксов.

Правда? Ну, делайте, как вам нравится.

В качестве компромисса давайте начнем эту главу, как мне нравится: с классической проблемы оптимизации, которую можно найти в любой книге по математическому анализу, начиная с «железного века» учебников по этой науке. Задача звучит примерно так: «Два положительных числа при умножении дают 100. Какой может быть их наименьшая сумма?»

Для начала мы можем попробовать различные пары чисел и посмотреть, что они дают в сумме.

Если первое число обозначить как A , то второе всегда равно 100, деленное на А (иначе говоря, 100/ А ). В результате получается следующий график:

Минимум находится там, где производная 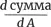точно равна нулю, что происходит, когда А = 10. Это означает, что второе число также 10, и, таким образом, минимальная сумма – 20. Выпейте безалкогольного шипящего сидра – задача решена!

Эта задача приятна и аккуратно подстрижена, как придомовая лужайка в пригороде. Вы исследуете возможности. Вы взвешиваете варианты. И в конце вы приходите к единственному решению – триумф равновесия и эффективности. Почему авторы книг по самосовершенствованию и IT-компании так активно призывают нас к «оптимизации». Если понимать ее буквально, оптимизация призвана делать вещи лучше. Кто, за исключением поклонников сериала «Звездный путь: Вояджер», предпочтет худшее лучшему?

Но это только одно понимание оптимизации. Сразу за углом скрывается дикий мир. Позвольте себе нечто простое и безрассудное – сделайте наоборот. Вместо того чтобы искать минимальную сумму, найдите максимальную .

Если подбирать правильные пары множителей, сумма может расти и расти, так, что мы потеряем над ней контроль, и раздуется до бесконечности, как обещания политика или вопли младенца. Как может понять любой избиратель или родитель, мы попали в кошмар оптимизатора. Никакого максимума здесь нет, только беспредельный, бесконечный подъем.

В 2003 г. философ Ник Бостром написал эссе об этических последствиях применения искусственного интеллекта, существенно превосходящего человеческий. Он включил в работу краткое описание того, как даже самая возвышенная цель при не испытывающем колебаний руководстве может привести к варварскому уничтожению всего, подобно графику, устремленному в бесконечность. Этот замысел в стиле фильма ужасов с тех пор вошел в обиход и воображение людей.

Я даю вам… Умножитель скрепок для бумаги.

Как в басне Эзопа «Черепаха и технологическая сингулярность [25] Гипотетический момент в развитии технологий искусственного интеллекта, когда человечество теряет над ними контроль. – Прим. ред. », мораль этой сказки совершенно ясна: никогда не создавайте силу, которой безразлично ваше выживание и которую вы не можете остановить. «Искусственный интеллект не испытывает к вам ненависти, – говорит философ Элиезер Юдковский, – не ощущает и любви, но вы сделаны из атомов, которые он может использовать для своих нужд».

Действительно ли существует эта угроза? Не сойдут ли через несколько секунд поезда с рельсов или это всего лишь зарисовка на ноутбуке градостроителя? Математик Ханна Фрай склонна придерживаться последней точки зрения. «Возможно, было бы куда более полезно подумать о том, как мы пройдем через революции в вычислительной статистике, чем через революцию в искусственном интеллекте, – пишет она в своей книге «Привет, мир! Оставаясь человеком в эпоху алгоритмов» (Hello World: Being Human in the Age of Algorithms). – Честно говоря, мы очень далеки от создания интеллекта даже на уровне ежика. Никто пока что не продвинулся дальше червя». Другие настроены менее оптимистично. «Часто случается, – пишет Юдковский, – что от ключевого технического изобретения, которое, казалось, появится только через несколько десятилетий, нас отделяет всего пять лет».

Стоит спросить: почему мы с вами не ведем себя как Умножитель скрепок? Я встречал людей – черт, да я сам бывал таким! – чьи цели были сомнительными или даже хуже. Мы способны на моральную слепоту, эгоистичную жадность и, когда стоим в медленно двигающейся очереди в магазине, на внезапный порыв кого-нибудь убить. Если Умножитель скрепок уничтожает мир ради глупой цели, почему мы с вами не уничтожаем мир, принимая во внимание, что наши цели являются далеко не возвышенными?

Отчасти дело в том, что нам просто не хватает сил. Но, кроме того – и это звучит более утешительно, – мы устроены сложнее и потому не способны так несгибаемо, не зная сомнений, идти к подобной цели.