Бен Орлин - Время переменных. Математический анализ в безумном мире

Такими были условия самой известной античной задачи на максимизацию. Какой участок земли вы можете отгородить с помощью некоторого количества длинных полосок кожи?

Эта загадка сегодня известна как изопериметрическая задача : приставка изо- здесь означает «тот же самый», а периметр – «подлая леди». По этимологическому совпадению периметр также означает «длина границы плоской фигуры».

Вопрос состоит в том, как можно захватить наибольшую площадь из всех возможных форм.

Не знаю, какими единицами длины пользовалась Элисса. Вероятнее всего, не метрами, если только она не была одной из первых, кто их применял. Поэтому, скажем, ее полоски соответствовали 60 «бычьим футам» (каждый из которых равен «1/60 общей длины, имевшейся у Элиссы»).

Теперь упорядоченная система геометрии предоставляет бесконечное разнообразие форм для города Элиссы.

Чтобы избежать такого разброса (и сложных расчетов площади), давайте возьмем самый простой класс фигур – прямоугольники.

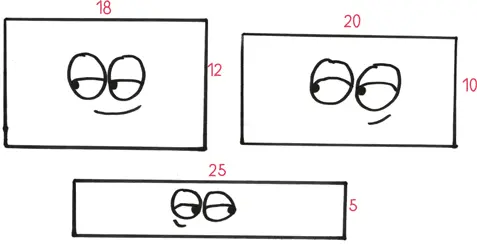
Имея шкуру быка определенного размера, Элиссе предстояло пойти на сделку. Чем больше она будет расширять основание прямоугольника, тем меньше будет высота, и наоборот. Увеличьте одно из измерений с 17 до 18, и другое тут же понизится с 13 до 12.

Мы можем иначе сформулировать формулу площади прямоугольника: не «ширина × высота», а «основание × (30 – основание)».

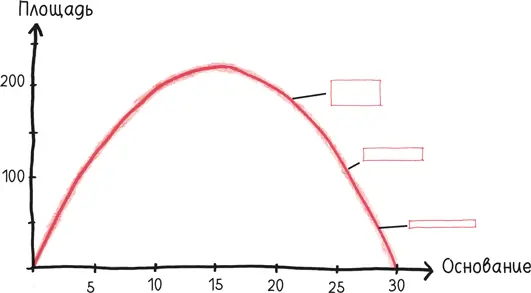
На графике сверху каждая точка обозначает возможный прямоугольник, зарождающуюся империю Элиссы. На левом краю находятся глупые планы, такие как 1 × 29, на правом – их зеркальные отражения, скажем 29 × 1. Благодаря каждому из них получается очень узкая территория площадью 29 квадратных единиц, зауженная до такой степени, что даже Бостон покажется просторным.

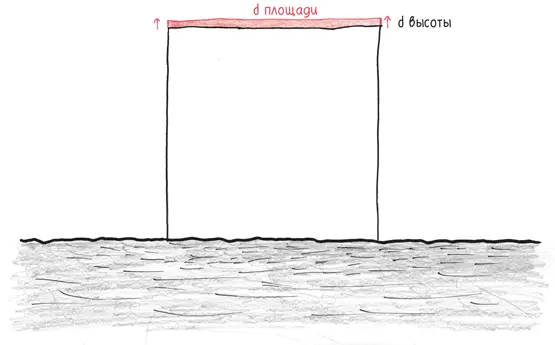
Почему получаются такие нежизнеспособные результаты? Просто рассмотрите производные. Отношение 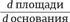скажет нам о том, как площадь реагирует на изменение основания.

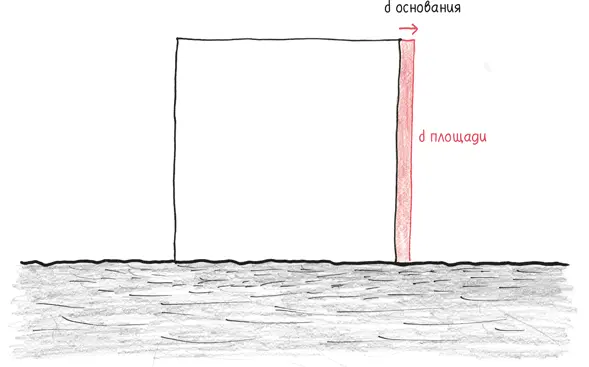
Тем временем 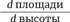скажет нам, как площадь реагирует на изменение высоты.

Увеличьте основание, и площадь чуть-чуть изменится. Увеличьте высоту, и она взлетит ввысь. Если пользоваться другими терминами, 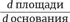ничтожно мало, в то время как 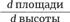огромно. Это порок всех подобных прямоугольников, напоминающих по форме спагетти, с удлиненным основанием и хилой высотой. По такому замыслу почти вся драгоценная бычья шкура уйдет на прижимистую производную, не оставив ничего щедрой.

Более умный план? Тратить, пока производные не станут равны. Это произойдет, как показывает график, когда стороны станут равны, в квадрате 15 × 15.

Решили ли мы проблему Элиссы? Не пора ли перерезать красную ленточку и начать занимать места на парковке? Не так быстро – у принцессы в запасе есть еще один трюк. Вместо того чтобы раскладывать полоски из бычьей кожи по открытой равнине, что, если ей отгородить участок на побережье Средиземного моря? Таким образом, вместо того чтобы выкладывать четыре стороны, ей понадобятся только три.

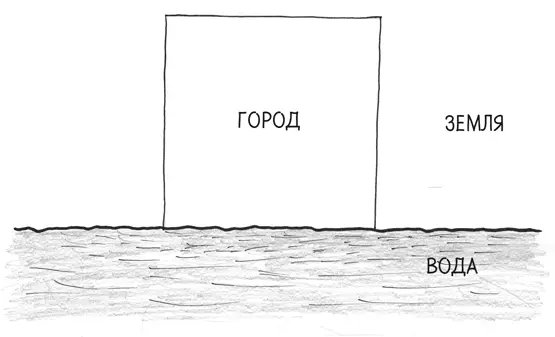
Ранее Элисса могла позволить себе квадрат 15 × 15. Сейчас она может отгородить область 20 × 20. Площадь увеличивается с 225 единиц до 400, город обрастает пригородами. Теперь-то мы уже можем выбирать мэра и, наконец, начинать жаловаться на строительство?

Однако, чтобы проверить, вернемся к производным. Вот что говорит нам 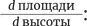самое маленькое увеличение высоты дает увеличение площади на 10 таких единиц.

Не так уж плохо! И можно предположить, что то же самое происходит с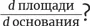

Черт возьми! Дополнительное приращение основания увеличит площадь на 20 таких единиц. Производные не равны!

По результатам проверки это имеет смысл. Каждый маленький участок высоты тянет за собой две стены, тогда как каждый участок основания – только одну. Таким образом, ширина «дешевле» в два раза. Квадратная форма перераспределяет ресурсы: мы ищем форму, при которой обе производные равны.

Теперь пора перейти к другому графику:

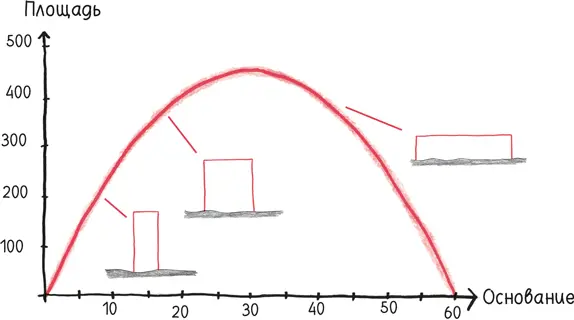
Оказывается, максимальную площадь займет прямоугольник 15 × 30, охватывающий 450 квадратных единиц.

Триумф, как ни крути! Элисса превратила свой перенаселенный Манхэттен из бычьей шкуры в просторный Хьюстон. Но, использовав кое-что под названием «вариационное исчисление», подразумевающее различные виды кривых, Элисса может получить больше площади от своих ничего не подозревающих партнеров по торговле. Это дает нам в действительности самое оптимальное решение – полукруг, диаметром которого является береговая линия.

Приблизительная площадь этой фигуры – 573 квадратные единицы. Совсем неплохо для оптимизации за один день.

Все это, как утверждают римские историки, произошло в конце IX в. до н. э. В последующие годы на полукруглом участке земли появился процветающий и сильный портовый город-государство под названием Карфаген. Он был могущественной державой, пока Рим не повел против него войны и, в конце концов, с трех попыток, не одолел его. Многие годы Катон Старший заканчивал каждую свою речь словами: «Карфаген должен быть разрушен» («Delenda est Carthago»), что, должно быть, звучало несколько странно, скажем, на открытии нового парка.