Бен Орлин - Время переменных. Математический анализ в безумном мире

В самые мирные моменты их медового месяца (а они отправились в недорогое стратосферное путешествие вокруг света) он пытался научить ее математическому анализу.

Он объяснял все, он объяснял все про все с самого начала до конца. Он объяснял так много, что она путалась, слушая его.

Как вымышленный персонаж, придуманный в 1948 г., Оона понятия не имела о том, что значит «самоутверждаться за счет женщины». Вместо этого она с радостью принимала уроки Джика и считала себя счастливицей. «Вот здорово! – думала она. – Множество мужей никогда не говорят со своими женами, только жалуются на плохую еду».

Однажды Джик пришел домой с великолепным подарком: «самым лучшим роботизированным мозгом, который когда-либо придумывали». Устройство называлось «визи-мат». Джик объяснил:

Ты пишешь на листочке любое математическое выражение, скармливаешь его машине… и получаешь перевод на язык визуальных представлений того выражения, которое тебя интересует.

В отличие от других подарков Джика визи-мат действительно помогает Ооне. И для высокотехнологичной машины вымышленного будущего он действует достаточно простым способом, показывая, как умножение связано с прямоугольниками.

Например, то, что 5 × 4 = 20, лучше всего можно понять, представив прямоугольник 5 × 4.

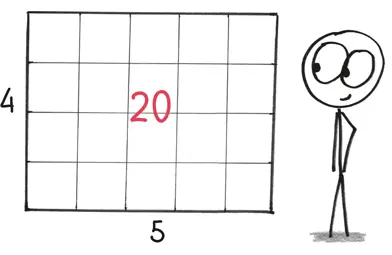
Это же работает и для умножения дробных чисел, скажем 6 × 2,5. Вы получаете 12 целых квадратов и шесть половинок, а всего – 15.

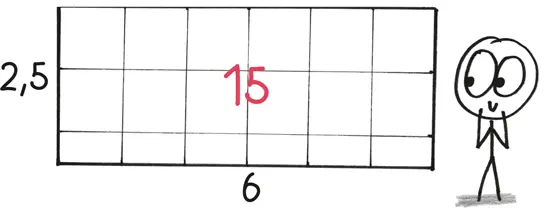
Так можно даже объяснить, как «возведение в квадрат» получило свое название, поскольку удвоение количества само по себе создает квадрат.

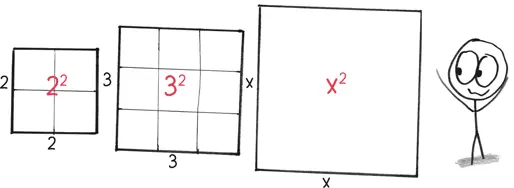
«Учить математике без иллюстраций – это преступление, – говорил Бенуа Мандельброт [22] Французский и американский математик, создатель фрактальной геометрии, лауреат премии Вольфа по физике. – Прим. пер. , – смехотворное занятие». Но каким-то образом такие учителя, как я, часто не могут следовать этому правилу. В том XXI в., где мы обитаем и где есть такие инструменты, как Wolfram|Alpha [23] База знаний и набор вычислительных алгоритмов, вопросно-ответная система, запущенная 15 мая 2009 г. – Прим. пер. и Desmos [24] Графический калькулятор, реализованный как приложение для браузера и мобильное приложение на языке JavaScript. – Прим. пер. , которые могли бы посрамить визи-мат, мы в своей профессиональной деятельности остаемся теми же Джиками.

Возьмем одно из первых правил курса математического анализа: производной функции х 2является 2 х . Должен отметить, что, объясняя ученикам этот факт, я всегда шел по алгебраическому пути:

Почему я продолжаю оставаться Джиком? Неужели стандартизированное обучение неумолимо ведет к механическому запоминанию? Или это связано с тем, что мы, учителя, не знаем хороших наглядных материалов, так как сами являемся продуктами системы? Или это затянувшееся влияние Бурбаки, радикальной группы математиков ХХ в., чей боевой клич «Смерть треугольникам!» предупреждал, что визуальное восприятие вводит в заблуждение, а абстрактный символизм – единственная твердая почва под ногами?

Какой бы ни была причина, визи-мат предлагает альтернативу. Начнем с возведения в квадрат, умножения х на х .

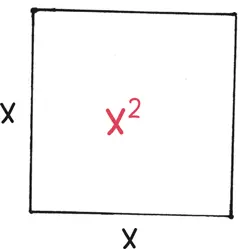
Производная, как вы, возможно, помните, – мгновенный уровень изменения. Следовательно, необходимо задать вопрос: «Если мы немного изменим х , на сколько изменится х 2?»

Так давайте пойдем вперед и немного увеличим х , назвав это dx .

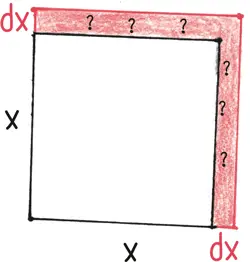
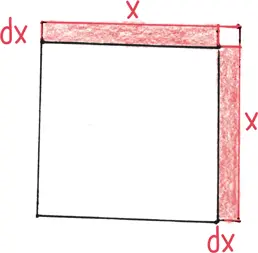
Рост х 2происходит в трех областях: двух длинных, тонких прямоугольниках (каждый х увеличивается на dx ) и в крошечном квадратике в углу ( dx на dx ).

Здесь мы остановимся, чтобы порассуждать о природе миниатюрности. Примерно так: вот это маленькое, а это просто крошечное. Скажем х = 1, а dx = 1/100. Это достаточно мало, верно? Конечно, но ( dx ) 2в сотню раз меньше: всего лишь 1/10 000. Это такое крошечное значение, что предыдущее по сравнению с ним выглядит огромным.

А если dx еще меньше, например 1/1 000 000? Тогда ( dx ) 2в миллион раз меньше и равняется только 1/1 000 000 000 000. Это новый уровень миниатюрности.

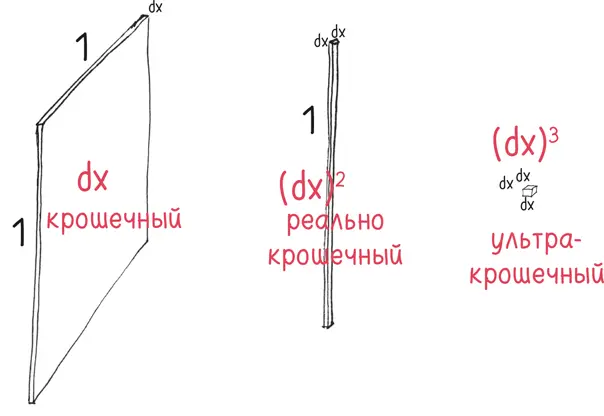
Что же представляет собой dx в действительности? Это стремящаяся к нулю величина меньше любого известного числа. (Джон Валлис, изобретатель значка бесконечности, записывал бесконечно малые величины как 1/∞, хотя ваш учитель может рассердиться из-за такого обозначения.) Так что ( dx ) 2не просто в сотню или миллион раз меньше, оно бесконечно меньше, это бесконечно малое от бесконечно малого. Оно с таким же успехом могло бы быть нулем.

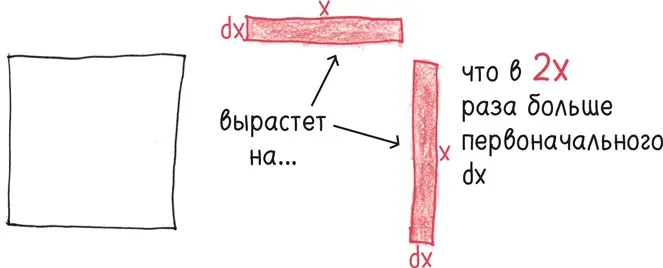
Так на много ли вырастет х 2? Если игнорировать пренебрежимо малое ( dx ) 2, он вырастет на два прямоугольника – один по ширине, другой по высоте.

Следовательно, производная равна 2 х .

Вернемся в гостиную будущего. Оона находит демонстрацию захватывающей.

Так вот что они имели в виду, когда говорили о возведении числа в квадрат! Не просто умножение его на себя самого или что там Джик говорил, но превращение числа в самый настоящий квадрат… Тогда математика – это не просто набор цифр, букв и глупостей. Она что-то значит, а математическое выражение, как предложение, о чем-то говорит.

Возбужденная Оона погрузилась в следующий демонстрационный пример визи-мата. Как может с зевком или всхлипом подтвердить любой студент-математик, производная х 3 – это 3 х 2. У Ооны – и у меня, и у моих студентов, и, черт побери, у любого человека, который когда-либо подвергался алгебраической пытке вроде той, которую устроил ведомый благими намерениями Джик, – возникает один вопрос: «Почему?»