Бен Орлин - Время переменных. Математический анализ в безумном мире

Чудо математического анализа, неизмеримая тайна всей этой науки в том, сколь многое переживает этот смертельный скачок. И производная, и интеграл ограничены пределами. Тем не менее они не прекращают свое существование. Они работают.

Такие загадки, как та, что нам загадала Брайанна, стимулировали развитие математики в XIX в. Целое поколение ученых совместно работало, чтобы раз и навсегда разгадать парадоксы в математическом анализе. Это означало превращение интуитивной, геометрической работы их предшественников в нечто четкое и нерушимое, в переосмысленный математический анализ, который сохраняет некоторые первоначальные черты, но избавляется от других.

Именно так обстоит дело с предельными процессами. Что-то исчезает, как осенние листья, что-то остается, как ветви деревьев зимой.

Год 1827. Наш главный герой – веселый седовласый ботаник по имени Роберт Броун. Он склоняется над микроскопом, вглядываясь в предметное стекло с пыльцой, – занятие, которое за десятки лет до появления кабельного телевидения можно было считать развлечением по выходным. Броун замечает нечто непривычное.

Танцевальную вечеринку в миниатюре.

Крошечные частицы зернышек пыльцы колеблются перед его глазами. Они танцуют джиттербаг [19] Джиттербаг – популярный в 1930–1950-е гг. танец с характерными быстрыми, резкими движениями, похожий на буги-вуги и рок-н-ролл. – Прим. пер. . Они исполняют джайв [20] Джайв – танец афроамериканского происхождения (разновидность свинга), появившийся в США в начале 1940-х гг. – Прим. пер. . Они подпрыгивают, как зерна кукурузы на горячей сковородке, или как накачанные кофеином кролики, или как я на свадебной вечеринке у друга. Они извиваются, как будто слышат песню «Uptown Funk». Что же поддерживает эту неистовую активность?

Возможно, это жизненная сила пыльцы, похожее на перемещение сперматозоидов вечное движение половых клеток растений? Нет. Начнем с того, что, даже если жидкость стоит в закрытом сосуде целый год, танец так и не останавливается. (Реальная проверка танцевальной вечеринки!) Далее Броун обнаруживает такое же движение у частиц стекла, гранита, дыма и даже пыли, собранной с великого сфинкса в Гизе, из чего мы можем сделать вывод, что в те времена туристы запросто могли поскрести исторический памятник, чтобы собрать бесплатные образцы для опытов.

Броун был не первым, кто обнаружил это явление. Поколением раньше ученый по имени Ян Ингенхауз заметил, что частицы угля трепыхаются в алкоголе. Почти за 2000 лет до этого римский поэт Лукреций писал о пыли, дрожащей в луче света. Это древний вездесущий танец.

Так что же он собой представляет?

Итак, весь мир состоит из атомов. Они находятся в постоянном движении. Без электронного микроскопа атомы мы увидеть не можем, но можем заметить более крупные частицы, которые атомы все время бомбардируют, – частицы, такие как пыль со сфинкса и пыльца цветов. Представьте себе огромный шар в парке Дисней Эпкот [21] Тематический парк развлечений во Флориде, посвященный технологическим новшествам. – Прим. науч. ред. , который непрерывно бомбардируют миллиарды невидимых маленьких шариков, и вы уловите эту идею.

В любой отдельно взятый момент совершенно случайный удар с одной стороны немного перевешивает удар с противоположной. Это вызывает отклонение частицы в одном направлении. В следующий момент схема меняется и частица движется в другом направлении.

Это продолжается вечность, момент за моментом, мгновение за мгновением.

Джига частиц, получившая название «броуновское движение», приводит в замешательство. Это движение частиц беспорядочно, то есть частицы не отдают предпочтения каким-либо направлениям. Оно непредсказуемо, иначе говоря, прошлые движения не дают никакой подсказки, в каком направлении частица будет двигаться в дальнейшем. Но, возможно, самое необычное из всего – это характер изменения направления.

Эти изменения в нашей математической модели являются недифференцируемыми .

Термин требует дополнительных разъяснений, поэтому представьте себя бейсбольным мячом. Я бросаю вас в воздух со скоростью 25 м/с. Предположим, вы простили мое агрессивное поведение, и мы вместе задаемся вопросом, что же происходит после этого. Вы пронзите атмосферу и отправитесь в долгое одинокое странствие среди звезд?

Боюсь, что нет, мой простроченный красными нитками друг! Вы житель Земли, попавший в гравитационную ловушку планеты. Поэтому через секунду вы замедлитесь до 15 м/с. Еще через секунду ваша скорость упадет до 5 м/с. А через следующую половину секунды вы замедлитесь еще сильнее, пока, наконец, не измените направление и не начнете падать с ускорением в направлении земли.

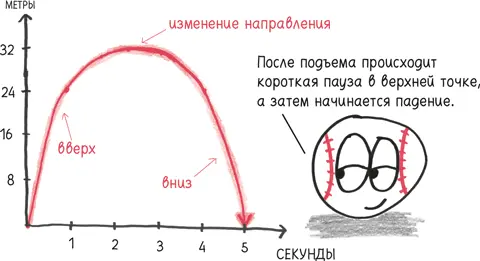
В верхней точке траектории нас ждет необычный и удивительный момент, когда вы уже перестали подниматься, но еще не начали падать. В этот краткий «чих» времени вы лишены движения, «путешествуете» со скоростью ноль метров в секунду.

А что, если мы снабдим вас ракетными ускорителями? Если когда-то вы были всего лишь просто шаром из воловьей кожи, то теперь стали оснащенным реактивным двигателем шаром из воловьей кожи. С помощью реактивной тяги вы взмываете вверх, а потом несетесь вниз. Не является ли это другим видом перемены направления?

На самом деле нет. Разумеется, то, что когда-то занимало целую секунду, теперь происходит за какие-то ее доли, но общая схема сохраняется. После того как ваше движение вверх замедлилось, и до того, как началось движение вниз, существует единственный момент смены направления, когда ваша мгновенная скорость равна нулю.

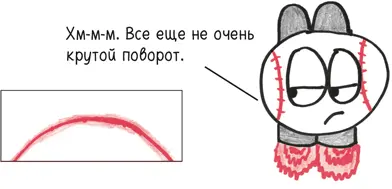
Только если очень напрячь свое математическое воображение, мы можем представить другой вариант развития событий, скажем, такой: