Бен Орлин - Время переменных. Математический анализ в безумном мире

– Правильно, – соглашается она. – А чему состоящая из точек часть равна сейчас ?

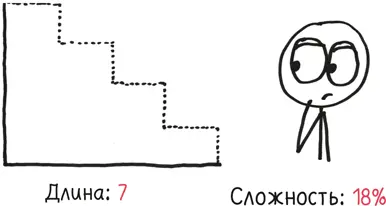
– Все еще семь. По той же логике.

Она чертит снова:

– А сейчас?

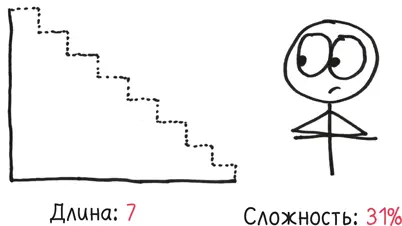
– Семь…

– Хорошо, а если мы будем делать бесконечно малые шаги по этой лестнице и у нас получится такая форма?

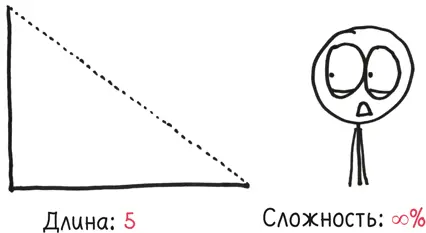
Я нахмурился. Это теорема Пифагора, самое старое правило практически в любом учебнике: a 2+ b 2= c 2. В этом случае если а = 3, а b = 4, то с = 5. Я так и сказал.

– Пять. Да, точно. – Брайанна наставила на меня карандаш, как микрофон. – А что здесь происходит?

В гостиной находятся следующие люди: (1) муж Брайанны Тайлер, в прошлом преподаватель математического анализа, а ныне предприниматель в сфере интеллектуального анализа данных, (2) моя жена Тарин, математик-исследователь, и (3) я, человек, который пишет книгу о математике. На троих у нас более 40 лет изучения математики и научные степени, полученные в Массачусетском технологическом институте, Калифорнийском университете в Беркли и Йеле. Мы все знаем всё о пределах и сходимости бесконечного ряда, о геометрии аппроксимации. Мы знаем, что семь не равно пяти.

Но перед этой задачей мы теряемся. Я чувствую себя так, словно мироздание меня одурачило – подкралось со спины и хлопнуло по левому плечу, чтобы я посмотрел не в том направлении. Я, кажется, слышу его хихиканье. Или это просто шум ветра.

– Неравномерная сходимость? – таинственно бормочет Тарин под нос.

– Нет четких пределов, – говорит Тайлер несколько неуверенно.

У меня самого в голове крутится несколько возможных опровержений в пику мирозданию, но ни одно из них ни капельки ничего не проясняет и не объясняет.

Все, что я могу сказать:

– Ух!

Загадка Брайанны нацелена в самое сердце математического анализа, в основополагающее философское понятие под названием предел . Предел – это конечный пункт назначения бесконечного процесса. Вы не обязательно достигнете предела: вы подходите к нему все ближе и ближе – ближе, чем это можно описать или вообразить. Брайанна в своей загадке установила по-настоящему «скользкий» предел. Он неким парадоксальным образом указывает сразу в двух направлениях. На каждом этапе длина равняется семи, а потом каким-то образом в самом конце вечности она становится пятью.

Подобные парадоксы давно одолевают математический анализ. Поколение спустя после того, как Готфрид Лейбниц и Исаак Ньютон впервые разработали эту часть математики, Джордж Беркли устраивал им трепку за небрежный образ мыслей. Ньютон требовал пристально изучать значения не до того, как они исчезнут (когда они все еще являются конечными числами), не после этого (когда они равны нулю), но когда они исчезают. Что он имел в виду?

«А что это за… исчезающие бесконечно малые? – глумился Беркли. – Они не являются ни конечными, ни бесконечно малыми величинами, ни даже ничем. Может быть, мы не будем называть их призраками былых величин?»

Парадокс Брайанны далеко не единственный. Другой вариант начинается с равностороннего треугольника. Если предполагать, что все три стороны равны, то путь по красным линиям в два раза дольше, чем по черной.

Далее возьмем две красные стороны, разделим каждую из них пополам, и, таким образом, наш путь вверх и вниз превратится в вверх-вниз-вверх-и-вниз.

Длина красной части не изменилась: мы просто перераспределили участки. Таким образом, они по-прежнему равны удвоенной длине черной стороны. И мы можем повторять и повторять этот процесс – делить и перераспределять, делить и перераспределять, а красный участок будет оставаться равным двум черным на всех этапах.

Если мы будем повторять деление бесконечное количество раз, то первоначальная красная треугольная «палатка» превратится в прямую линию из пылинок, неотличимую от черной. Но… не привело ли это к тому, что путь вырос в два раза?

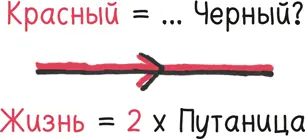
Исследователям потребовались столетия ложных шагов и осечек, чтобы разобраться с этой проблемой. «Чтение трудов математиков этого периода, – пишет профессор Уильям Данхэм, – напоминает прослушивание произведений Шопена, которые исполняются на пианино, где несколько клавиш расстроены: в один момент можно оценить гениальность музыки, а в другой она режет слух».

Ставящая в тупик правда – она сбивает с толку не меньше, чем несомненная простота этой проблемы, – состоит в том, что не ко всему можно применять предельный переход.

Возьмем последовательность 0,9; 0,99; 0,999; 0,9999… На каждом этапе мы получаем дробь – нецелое число. Но каким-то образом на вымощенной желтым кирпичом дороге к бесконечности последовательность превращается в единицу.

Означает ли это, что единица не является целым числом? Черт побери, нет! Это просто значит, что конечная точка движения не обязательно должна напоминать путь, который привел вас к ней. Деревянные ступеньки могут привести к лестничной площадке, покрытой ковром.

Вот пример, который моя жена приводит на первых занятиях по математическому анализу: треугольная волна, двигающаяся через плоскость вдоль оси х .

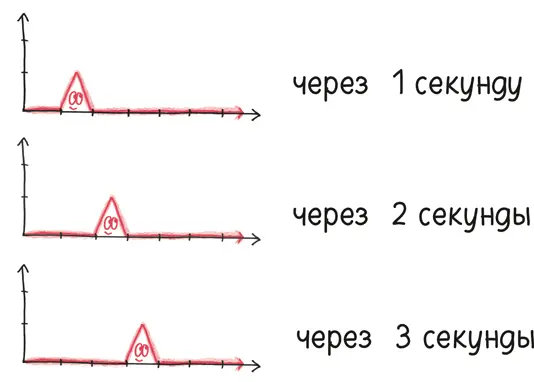
Каждая точка в какой-то момент является нулем, затем на короткий период времени, во время прохождения волны, она не равна нулю, затем это снова нуль, навеки и даже дольше. Каждая точка, таким образом, рано или поздно приближается к нулевой отметке. Это означает, что пределом всего сценария является горизонтальная линия, ось х .

Но что происходит с волной? Не стирает ли ее предел с лица земли, как нейтронная бомба?

Одним словом, да. Пределы могут это сделать.

В действительности вы никогда не «достигнете» предела. Приблизиться к нему вы, конечно, можете – так близко, что почувствуете его запах, его боль, но коснуться его не удастся. Прыжок к пределу – это трансцендентальный акт, это сродни переходу к смерти: скачок от подвластного времени тела к существующей вне времени душе. Почему любая принадлежащая нам вещь должна пережить это путешествие? У наc есть волосы и зубы, но разве мы ожидаем, что после смерти будем существовать в виде волосатых и зубастых духов?