Бен Орлин - Время переменных. Математический анализ в безумном мире

Слово «касательная» происходит от латинского tangere («касаться», «трогать»), как и слова tangible («осязаемый», «ощутимый») и «танго»; все эти слова связаны с проявлениями нежности и прикосновениями. В математике касательная совпадает с кривой в одной точке. Так она на какое-то мимолетное мгновение принимает относящееся к конкретному моменту направление кривой, ее производную.

Например, если кривая изображает путь машины, то касательная будет указывать направление света фар.

Или, для более наглядной демонстрации, привяжите веревку к камню, раскрутите его над головой и подождите, пока веревка порвется. Камень полетит по прямой: касательная – это его путь в момент разрыва.

А что же насчет велосипеда? Поскольку заднее колесо закреплено на раме, в любой отдельно взятый момент оно гонится за передним. Другими словами, его направление в конкретный момент движения указывает туда, где находится переднее колесо.

Давайте проверим этот факт при помощи приведенной ранее загадки. Без каких-либо подсказок о глубине следа можем ли мы определить, где отпечаток переднего колеса?

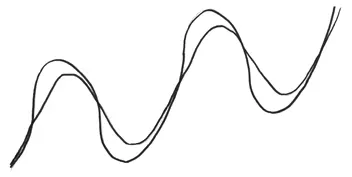
Элементарно, мой дорогой Холмс! Просто найдите момент вдоль одной из линий, когда касательная указывает в пространство, в направлении, куда велосипед никогда не ехал. Могло ли заднее колесо повернуться туда? Никогда! Оно всегда повторяет поведение переднего колеса. Таким образом, линия с направленными вовне касательными должна принадлежать переднему колесу.

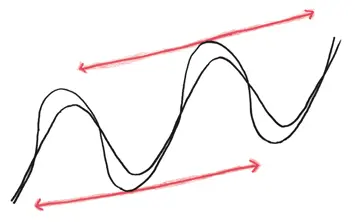
Теперь вопрос на 6000 фунтов – такое вознаграждение назначил герцог в рассказе: в каком же направлении двигается велосипед?

Есть только два возможных варианта. Во-первых, предположим, что велосипед двигается слева направо. Проведем соответствующие касательные для заднего колеса, продлив их до тех пор, пока они не пересекутся со следом переднего.

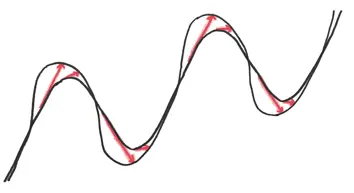
Расстояние от заднего до переднего колеса вдоль касательной должно соответствовать длине велосипеда. Но здесь это расстояние меняется от точки к точке. Нам остается только заключить, что во время своего путешествия велосипед менял длину, как двухколесная игрушка на пружине. Такой велосипед должен бы принадлежать ездоку, не имеющему себя равных в ловкости и обладающему сомнительным здравомыслием.

В «Случае в интернате» есть подходящий комментарий:

– Холмс! – воскликнул я. – Это неправдоподобно!

– Браво! – сказал он. – Вывод исчерпывающий. В моем изложении событий есть что-то неправдоподобное, следовательно, я допустил ошибку… Где же я ошибаюсь?

В нашем случае ошибка совершенно ясна. Мы не рассмотрели альтернативу – ведь велосипед мог двигаться справа налево.

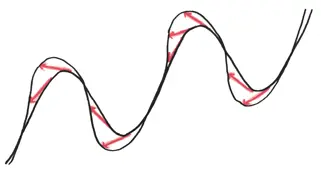
Ага! Эти касательные, к счастью, одной длины. Они говорят о велосипеде прочной конструкции, вполне правдоподобном. Значит, мы можем прийти к выводу, что велосипед двигался в этом направлении.

Разве это не замечательный ход мысли? Он позволяет увидеть за следами факты и, расшифровав язык геометрии, раскрыть истину. Тщательное изучение улик сочетается здесь с безупречным логическим анализом. Разве не в этом секрет триумфа гениального сыщика – и, в нашем случае, высшей математики?

Отношения Холмса с математикой вполне понятны – это его зеркальное отображение. Именно поэтому, когда Конан Дойлю хочется ввести в повествование антагониста, который станет противостоять наблюдательному сыщику, он придумывает математика профессора Мориарти. «Наполеон преступного мира» описывается как «гений, философ» и «абстрактный мыслитель», кроме того, он – «прославленный автор “Движения астероидов”, книги, затрагивающей такие высоты чистой математики, что, говорят, не нашлось никого, кто мог бы написать о ней критический отзыв» [16] Цит. по: Дойль, Артур Конан. Долина ужаса: Новые приключения Шерлока Холмса / Пер. А. Москвина. – М.: Кооператив АВИС: Прометей, 1990. .

Поневоле приходишь в уныние, стоит подумать, как быстро Мориарти разобрался бы в следах велосипеда. Соперник Холмса, можно быть уверенными, знал о касательных.

Я сам впервые узнал о загадке с велосипедом из прекрасной биографической книги «Гений играет: пытливый ум Джона Хортона Конвея» Шивон Робертс. В одной запоминающейся сцене команда из трех математиков собирается вести экспериментальный курс в Принстоне. Он представляет собой «подпольную, бунтарскую попытку», направленную на то, чтобы показать, что «математика и поэзия похожи», и называется «Геометрия и воображение». Ожидая, что на занятиях будет не более 20 студентов, преподаватели ошарашены, когда выясняется, что на курс записалось 92 человека. Как рассказывает Робертс, молодые люди не потратили свои деньги зря:

Преподаватели строго соблюдали ритуал и появлялись в классе все разом, иногда с большой помпой и важностью, порой они несли флаг, время от времени надевали велосипедные шлемы, часто тянули за собой детскую тележку, наполненную многогранниками, зеркалами, фонариками и свежими продуктами из продуктового магазина…

Для одного урока преподаватели «отыскали огромные рулоны бумаги, разорванные на полосы размером, по меньшей мере, 1,8 метра на 6 метров» и ездили по ним на велосипедах с вымазанными краской колесами. В результате получились эпические полотна геометрического велосипедного искусства, головоломки в натуральную величину. Студенты, как юные Шерлоки, получили задание определить, в каком направлении ехал каждый велосипедист.

Но преподаватели добавили деталь, которая, возможно, озадачила бы самого Мориарти:

Тем не менее часть из этих следов поставила студентов в тупик. Эту серию линий Питер Дойль [один из преподавателей] оставил на листе бумаги, когда ездил туда-обратно на велосипеде с одним колесом.