Бен Орлин - Время переменных. Математический анализ в безумном мире

Многие годы Пеннингс и Элвис вместе посещали различные мероприятия. В завершение каждого разговора Тим ставил Элвиса на стол перед аудиторией.

– А теперь внимательно следите за его глазами и ушами, – советовал математик.

Затем тихим и таинственным голосом он спрашивал:

– Элвис, какой будет производная от х 3?

Все глаза были устремлены на корги, а пес смотрел на Пеннингса, склонив голову.

– Видите это?! – восклицал профессор. – Видите, что он делает?

Еще одна многозначительная пауза.

– Он ничего не делает. Он никогда ничего не делает, когда я задаю ему этот вопрос.

Спойлер: собаки не владеют математическим анализом. Но естественный отбор – это мощное средство оптимизации. Чем быстрее собака сможет добраться до еды, тем выше ее шансы – и шансы ее детей – на выживание. Таким образом, со временем собаки, которые выбирают самые эффективные пути, начинают доминировать в популяции. Поколение за поколением собаки «учатся» математическому анализу. По той же самой причине шестиугольные ячейки сот уменьшают количество отходов, разветвление легких увеличивает площадь поверхности, а артерии млекопитающих минимизируют обратный кровоток. Природа каким-то странным образом владеет математическим анализом.

«Мы не знаем, почему Пеннингс так удивлен, – писали на сайте Национального дня чистопородных собак, – Элвис был псом породы вельш-корги пемброк, а мы все знаем, как ОНИ умны».

В самом деле, Элвис вскоре получил почетную докторскую степень колледжа Хоуп вместе с официальной грамотой и ярко-оранжевым капюшоном. Пеннингс сделал для Элвиса визитные карточки, но, пытаясь сократить латинскую фразу «собачий доктор наук», он случайно превратил ее в «собачий гинеколог». Вот таким получилось еще одно историческое удостоверение личности этой прокладывающей новые пути собаки.

В электронном письме Пеннингс поделился со мной своей коронной идеей, которую он вынашивал годами, – написать книгу под названием «Математика как ее понимают собаки». Снабженная фотографиями Элвиса книга должна была включать математический анализ (оптимизацию, относительные величины), высшую математику (бифуркации, теорию хаоса), некоторую часть гуманитарных наук, основные свойства построения моделей (иными словами, действительно ли Элвис начинает плыть, как только входит в воду? Да, потому что даже на мелководье его короткие 13-сантиметровые ноги не касаются дна)… и (это было во втором письме, которое пришло несколько мгновений спустя) урок скромности. Элвис, возможно, ничего и не знал о производной х 3, но пес-профессор многому может нас научить.

Элвис умер в 2013 г. «Никакой собаке не нравится приближение смерти, – писал Тербер, – но я никогда не видел, чтобы пес демонстрировал человеческий панический страх перед ней. Для собаки смерть – это последнее неизбежное принуждение, последний неотвратимый след, который уводит по зловещей тропе».

– Элвис начал свой путь как собака, которая действительно была хорошим другом, – сказал мне Пеннингс. – К тому времени, когда он умер, он был моим хорошим другом, которому просто случилось быть собакой.

Возможно, вы замечали, что в математике существует множество символов – разнообразный алфавит иксов, семерок и ■. В идеале тот, кто занимается математикой, должен знать, что эти символы означают: скрывается ли за х «пространство» или «время», указывает ли y на «годы» или «картофелины», говорит ли zzz о z 3или «храпе». Для каждого знака есть значение, но не для каждого значения есть знак.

Увы, «идеальный» – это не самое лучшее прилагательное для учебной аудитории. Скорее всего, вы обнаружите, что студенты делают заметки на страницах и зубрят все без всякого понимания, не возвращаясь к пройденному, пока процесс не доводится до автоматизма. Соедините иксы, уберите семерки, а если сомневаетесь, добавьте ■. Это все напоминает ведение бухгалтерского учета на языке, которым вы не владеете. Не важно «почему», единственный вопрос «как»: «Как я могу получить это из этого?» Здесь можно процитировать «Процесс» Кафки: «Мне кажется, тут, безусловно, есть что-то научное. Я, правда, мало что понимаю, но, наверно, тут и понимать не следует» [27] Кафка Ф. Процесс. – М.: Азбука, 2019. . При этом Кафка описывал тоталитарную бюрократию, а не мои уроки математики, но, как гласит народная мудрость, «что в лоб, что по лбу».

Каким же образом конкретное значение уступает чистой абстракции? Наберитесь храбрости, и я вам это покажу.

Начнем с дружелюбной физиономии прямоугольника со сторонами А и В . Его площадь является произведением этих сторон АВ .

Теперь представим, что его параметры меняются со временем, как у города, год за годом разрастающегося на север и на восток. Ширина ( А ) растет со скоростью А ´, а длина ( В ) – со скоростью В ´.

Вопрос: как быстро увеличивается площадь АВ ?

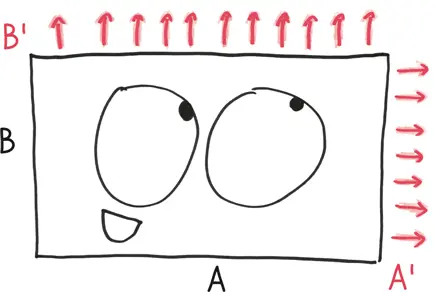
Это математический анализ, то есть мы размышляем об отдельно взятом моменте. В это летучее мгновение ширина увеличивается на бесконечно малую величину (которую мы можем назвать dA или А ´), и длина делает то же самое (соответственно, при этом получается dB или В ´).

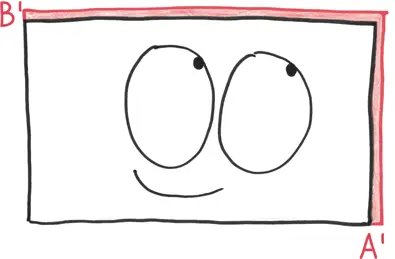
Мы можем разделить эту зону роста на три части: (1) длинная тонкая полоса справа, (2) еще одна сверху и (3) крошечный квадратик. Этой умилительной третьей частью можно пренебречь по причинам, описанным в главе X; если каждая тонкая полоска имеет толщину человеческого волоса, то квадратик имеет площадь, как у одной-единственной клетки. Мы можем исключить его из наших расчетов.

Теперь определим, насколько велики две оставшиеся зоны роста. С рисунком это очень просто: одна – произведение А ´ на В , а другая – В ´ на А .

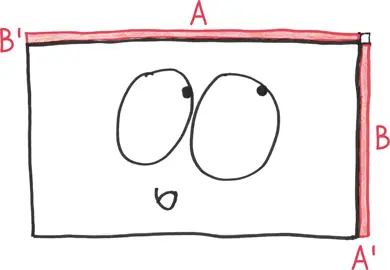
Таким образом, размер зоны роста – это сумма площадей двух полосок.