Бен Орлин - Время переменных. Математический анализ в безумном мире
- Название:Время переменных. Математический анализ в безумном мире
- Автор:
- Жанр:
- Издательство:Литагент Альпина
- Год:2021
- Город:Москва
- ISBN:9785001394525
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Бен Орлин - Время переменных. Математический анализ в безумном мире краткое содержание
Тема движения времени находит отражение и в названиях частей книги – «Мгновения» и «Вечности», и в ее персонажах – от Шерлока Холмса до Марка Твена и Дэвида Фостера Уоллеса. C присущими ему юмором и изобретательностью Орлин выявляет связи между матанализом, искусством, литературой и любимой собакой по имени Элвис.
Автор нашумевшей «Математики с дурацкими рисунками» и в этой книге ставит своей целью не просто увлечь читателя любимым предметом, но сделать нас более мудрыми и вдумчивыми.
Время переменных. Математический анализ в безумном мире - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
В наши дни все вокруг действительно стало подвидом матана.

«Если бы история пошла по другому пути, – пишет Вольфрам, – то можно было бы провести прямую линию от Лейбница к современным компьютерам». В нашей реальности путь получился более извилистым. Прорывные открытия, сделанные Лейбницем в XVII в., привели к золотому веку символьных вычислений в XVIII в., которые, в свою очередь, в XIX в. вызвали обратную реакцию, когда все были одержимы аксиоматизацией и математической строгостью. В ХХ в. это вылилось в работу над формальными системами и вычислимостью, в результате чего в XXI в. появился ноутбук, на котором я сейчас печатаю это бессвязное предложение.
Побежден ли Лейбниц или ему удалось отстоять свою правоту? Живем ли мы в мире, история которого отрицает ученого? Или вокруг нас находятся его мечты? Подозреваю, что есть только один способ узнать это. Берите бумагу и ручку, друг мой. Посчитаем!
Послушай, Капля, отдай себя без сожаления, и взамен ты достигнешь океана.
РУМИВечности

XVI
В литературных кругах
Коктейльная вечеринка. Напиток в руке, светский разговор, можно разглядывать красивых девушек. Все это довольно приятно, пока кто-нибудь не спросит, чем я занимаюсь. Если смотреть на то, как меняются лица собеседников во время моего ответа, можно подумать, что я говорю: «Я член мафии», или «Я коррумпированный судья», или «Я путешественник во времени, которого послали предотвратить апокалипсис, для чего надо убить всех присутствующих на этой вечеринке».
В действительности я отвечаю: «Я учитель математики».

Понятно, мы с коллегами не всегда воздаем должное красоте нашего предмета. Я говорю слово «круг», и немногие студенты вспоминают стихи Джона Донна: «Но если ты всегда тверда / Там, в центре, то должна вернуть / Меня с моих кругов туда, / Откуда я пустился в путь» [29] Донн Дж. Прощание, запрещающее грусть / Пер. И. Бродского.
– или представление Паскаля об устройстве Вселенной: «Вселенная – это не имеющая границ сфера, центр ее всюду, окружность – нигде» [30] Паскаль Б. Мысли. – М.: Изд-во имени Сабашниковых, 1995. – С. 132.
. Нет, в голову приходят наполовину заученные формулы. Задачи из учебника. Бесконечные цифры после запятой в числе π.
Я чувствую себя обязанным защитить честь своего предмета, доказать, что он принадлежит к перекрывающим друг друга кругам Эйлера. Поэтому я делаю то, что сделал бы любой на моем месте: со скоростью голодного зверя хватаю порцию еды со стола с закусками.
– Какова площадь этого куска огурца? – требую я ответа.

Тот, кто бросил мне вызов, хмурится:
– Это странный вопрос.
– Вы правы! – кричу я. – Это странный вопрос, потому что площадь определяется с помощью крошечных квадратиков – квадратных дюймов, или квадратных сантиметров, или даже квадратных миллиметров, – а этот круглый ломтик огурца не может быть разделен на квадратики. Из-за закругленных краев его площадь трудно измерить. Поэтому… что же нам делать?
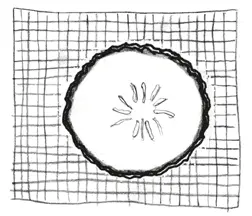
В этот момент я вооружаюсь ножом. Возможно, мой собеседник пугается, но, если мне повезет, он увидит, что я имею в виду.
– А! – восклицает он. – Мы можем порезать его на кусочки!
И мы режем несчастный огурец, как крошечный пирог, так, чтобы получилось восемь маленьких ломтиков. Расположив их иначе, мы получаем фигуру другой формы, но имеющую ту же площадь, что и первоначальный кусок огурца.
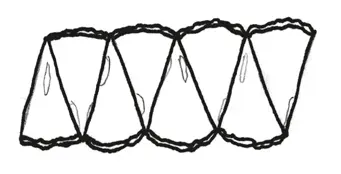
– Это почти прямоугольник, – отмечает мой оппонент. – А площадь прямоугольника найти просто. Нужно только умножить его высоту на ширину.
– Так какой же будет высота и ширина? – спрашиваю я.
– Ну, ширина – это, должно быть, половина длины окружности огурца. А высота, наверное, радиус огурца.
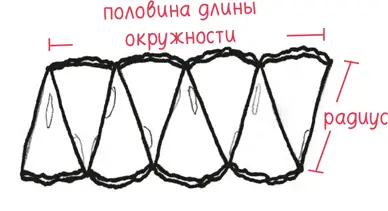
– Так задача решена?
– Не-а, – отвечает он. – На самом деле это не прямоугольник. Он неровный. Искаженный.
– Специальный термин, – объясняю я, – это «колеблющийся». Так что же нам делать?
Размышляя в этом направлении, мы берем еще один кусок огурца и рассекаем его на 24 еще более тонких ломтика. После их тщательного раскладывания получается фигура подобной формы, только слегка менее колеблющаяся, чуть менее шатающаяся. Другие гости смотрят на нас с благоговейным страхом и восхищением или, возможно, с жалостью и отвращением – я никогда не мог определить разницу.
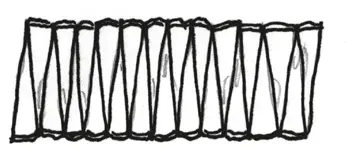
– Теперь он более прямоугольный! – говорит мой собеседник. – Но еще не совсем.
Так что мы берем еще один ломтик огурца и нарезаем его еще тоньше.

– Теперь это прямоугольник? – спрашиваю я.
Вздох:
– Нет. Он все еще колеблется по высоте и шатается по ширине. Все эти загибы здесь, пусть даже они стали микроскопическими.
– Специальный термин, – объясняю я, – это «малипусенький».
– Надо нарезать огурец на неисчислимые ломтики, каждый из которых бесконечно мал, – говорят мне. – Это единственный способ создать прямоугольник. Но… это невозможно.
Мой оппонент колеблется:
– Не так ли?
Возможно это или нет, но математик по имени Евдокс сделал это еще 24 века назад, на территории, где в наши дни находится Турция. Мы называем такой подход «методом исчерпывания» не потому, что он что-то исчерпывает, а потому, что определенное расхождение постепенно исчезает, или «исчерпывается». Это расхождение между приближением (колеблющимся прямоугольником) и тем, к чему он стремится (идеальным, свободным от колебаний прямоугольником). Проследуем по этому логическому пути до конца, и мы увидим, что площадь круга – это то же самое, что площадь прямоугольника: произведение радиуса и половины длины окружности.
Или, если вы предпочитаете уравнения: 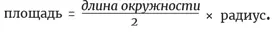
Интервал:
Закладка:









![Стивен Строгац - Бесконечная сила [Как математический анализ раскрывает тайны вселенной]](/books/1150749/stiven-strogac-beskonechnaya-sila-kak-matematicheski.webp)
