Бен Орлин - Время переменных. Математический анализ в безумном мире

На столовой салфетке мы набросали интеграл в зачаточном виде. Рассечь проблемный объект на неисчислимые части, каждая из которых бесконечно мала; переместить их, сложить более простую совокупность и из этого перемещения сделать выводы о первоначальном объекте – эти шаги формируют шаблон, наметки интегрального исчисления.

Возможно, к этому моменту у моего собеседника кончилось вино. Вполне справедливо. Мы обмениваемся кивками и визитными карточками, чтобы больше никогда не встречаться. Предполагаю, именно для этого визитные карточки и служат – всеобщий знак, заменяющий слова «прощайте навсегда!».

Или, возможно, любопытство моего оппонента только усилилось. Он снова наполняет мой бокал, я набиваю карманы сыром, и, глубоко вдохнув, мы снова погружаемся в математику.

– Крутая формула! – говорит он. – Но это не совсем то, что я учил в школе.

– Это потому, что мы определили площадь через длину окружности, – говорю я. – А мы еще не нашли, чему равна длина окружности.

– Так как же мы это сделаем?

Вначале мы совершим небольшой экскурс в историю. Основополагающий древнекитайский трактат по математике называется «Математика в девяти книгах». Я считаю, что давать ему такое прозаическое название было просто стыдно. Другие древнекитайские математические тексты называются как-то вроде «Эссе о бассейне мечты» или «Яшмовое зеркало четырех первоэлементов». Составлявшиеся в течение нескольких веков «Девять книг» содержат в себе всё – от арифметики до геометрии и операций с матрицами, это математическая библия, обладающая неизмеримой глубиной и полнотой.

Есть только одна проблема: в ней напрочь отсутствуют объяснения. Это просто набор процедур без малейшего намека на конкретные случаи или разработку. На мой взгляд, самый худший вид учебника.

Тут на сцену выходит математик III в. Лю Хуэй. Он не был автором «Математики в девяти книгах»; он написал к ним комментарии, совсем как принц-полукровка в романе Джоан Роулинг; он был вдумчивым читателем, снабдившим примечаниями старый пыльный текст и таким образом вдохнувшим в него новую жизнь.

Оригинальная книга обходила стороной вопрос о длине окружности. Лю Хуэй был не таким человеком, чтобы не обращать на него внимания. Идя по его стопам, я набираю горсть зубочисток из фруктовой нарезки и располагаю их в виде треугольника на огуречном кружке.

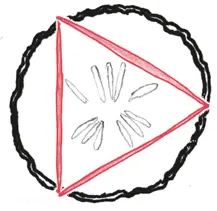
– Вот! – заявляю я. – Длина окружности!

Мой собеседник поднимает бровь.

– Каждая сторона треугольника, – объясняю я, – это 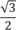длины диаметра. Таким образом, весь периметр – это 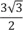или приблизительно 2,6.

– Но это периметр треугольника, – отвечает он. – Не окружности.

– Естественно, – отвечаю я. – Кто может измерить кривую? Мы только можем приблизить ее к прямым линиям.

– Ну, если таков ваш подход, – говорит он с усмешкой, – вам лучше закончить чем-то подобным.

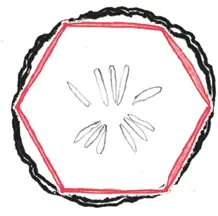
Быстрая перестановка удваивает количество сторон в моей фигуре с трех до шести.

– Шестиугольник, – заявляю я. – Да. Теперь периметр этой фигуры равен трем диаметрам. И это действительно длина окружности, не так ли?

Едва ли. Мы только воссоздали предположение из оригинальной «Математики в девяти главах». Тем не менее, если еще немного поделить и разложить, мы последуем за Лю Хуэем и получим фигуру с 12 сторонами.

Немного тригонометрических вычислений на коленке, и мы узнаем, что периметр 12-угольника равен 3√ –6 − 3√ –2, или приблизительно 3,11.

Уже лучше. Но все еще не длина окружности. Не точно .

«Делите снова и снова, пока не настанет момент, когда дальше делить будет невозможно, – писал Лю Хуэй. – В результате мы получим правильный многоугольник, вписанный в окружность, и не останется никаких пустых участков». На самом деле этот процесс никогда не завершится, но он приближает к истине. Зубочистки ломаются на все меньшие и меньшие кусочки, где-то в конце вечности процесс достигнет апогея, и у нас будет неисчислимое множество кусков, каждый из которых является бесконечно малым. Все вместе они составят длину окружности.

Лю Хуэй дошел до многоугольника со 192 сторонами. В V в. его последователь Цзу Чунчжи сделал даже больше – 3072 стороны, и это позволило ему добиться такой точности, которую в течение следующего тысячелетия не смог превзойти никто. Длина окружности, по оценке Цзу, составляла 3,1415926 диаметра.

Знакомые цифры?

Сегодняшние поклонники числа π, бурно отмечающие его день и страницами заучивающие знаки после запятой, не первые в своем страстном увлечении. В XV в. индийские и персидские исследователи заложили зачатки математического анализа, определив число π с точностью до 15-го знака после запятой. В 1800-х гг. упрямец Уильям Шэнкс потратил десять лет своей жизни на то, чтобы вычислить 707 знаков, причем первые 527 из них действительно оказались правильными. Сегодняшние суперкомпьютеры могут рассчитать число π с точностью до миллиардного знака; если все эти цифры распечатать, а страницы с ними переплести, то получится библиотека, по размеру сопоставимая с гарвардской и такая же скучная.

Если учесть, что ряд чисел бесконечен, мы нисколько не приближаемся к концу. И все эти знаки совершенно бесполезны, нам никогда не понадобится ни один из тех, что находятся дальше первых нескольких десятков. Так почему же число π так нас завораживает?

Причина, думаю, очень проста. Люди что-то видят, и людям нужно это измерить. Круг – это неотъемлемая и неподатливая часть нашей реальности, как масса Земли, расстояние до Луны или количество звезд в Галактике. Даже более неподатливая, чем другие, потому что число π не меняется со временем. Оно остается константой логического мироздания. Поэт и лауреат Нобелевской премии Вислава Шимборская посвятила числу π гимн. Она писала: «ибо небо и земля прейдут, / но не Пи, только не оно, / оно продолжается пять , / уходит восемь , / не останавливаясь семь , / стремя, о, стремя беспечную вечность / все дальше» [31] Пер. Т. Бонч-Осмоловской. – Прим. ред. .

Математики Античности рассекали окружность на неисчислимые куски, каждый из которых был бесконечно малым. Они делали это, чтобы лучше познать целое – площадь из клочков, длину окружности из обломков. Оглядываясь назад, мы можем распознать в этих попытках древних математиков то, чем они и являлись, – начало интегрального исчисления.