Бен Орлин - Время переменных. Математический анализ в безумном мире

Как ни грустно, 150 лет назад все произошло совсем по-другому.

В те дни никто на самом деле не ожидал открытия детерминированных законов истории. Вместо этого науки представлялись как расположенные в неоднородной последовательности от точных (таких как математика и физика) до гуманитарных (скажем, психологии и социологии).

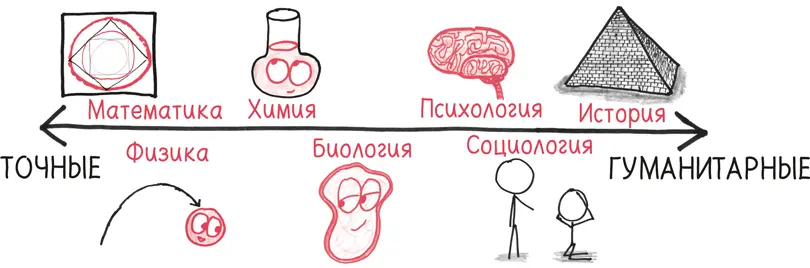
В своем самом невыносимом настроении точные науки любят хвастаться и злорадствовать, как будто точные означает сложные, а гуманитарные – простые. Дело, конечно, обстоит совсем наоборот. Чем «легче» наука, тем более сложным являются описываемые ею явления.

Физики могут предсказать поведение атомов. Но соберите достаточное количество атомов, и расчеты станут слишком громоздкими и тяжеловесными. Нам нужны другие, новые законы – химические. Затем соберите достаточное количество химических элементов, и сложность снова захлестнет нас. Чтобы перейти к новым теориям и правилам, нам понадобится биология, и так далее по этой прямой. В каждый переломный момент роль математики меняется: из доподлинной она превращается в ориентировочную, из детерминистической – в статистическую, из обобщенной – в противоречивую. Простые явления (такие как кварки) следуют математическим законам с рабской покорностью. Сложные феномены (например, маленькие дети) подчиняются им в гораздо меньшей степени.

О чем же просит Толстой? Ему не так уж много и надо: только того, чтобы самые сложные явления подпадали под действие самых строгих математических законов. Только чтобы люди вели себя, как планеты. Надо ли говорить, что мы все еще ждем появления этой теории.

В Толстом наблюдается противоречие: с одной стороны, он чуток к мелочам и обладает даром улавливать искрометные мгновения повседневной жизни. С другой стороны, его снедает желание получить ответы на глобальные вопросы: что движет людьми? Почему случаются войны? Отчего воцаряется мир? Интеграл – это мостик между даром Толстого и его мечтой. Предполагается, что он может соединить мир, который писатель знает (мешанину частных явлений деталей), и мир, которого он страстно желает (идеально управляемое королевство), чтобы сплавить бесконечное разнообразие с идеальным единообразием.

Интеграл Толстого не имел успеха как наука, но, думаю, был прекрасен как метафора. В такой схеме мира люди так малы, что их можно считать бесконечно малыми, и так многочисленны, что им практически нет числа. И тем не менее добавьте каждого из этих отдельных людей, и вы получите человеческую природу. Если следовать такой логике, история не принадлежит какой-либо группе или подгруппе – ни королям, ни президентам, ни богине воинов по имени Бейонсе, ни какой-то отдельно взятой леди, – но всем отдельно взятым леди.

История – это сумма всех людей, проживших ее.

Она не поддается ни научным прогнозам, ни математическим законам. Скорее, это поэтическая правда, художественная правда – но в сумме всех бесконечно малых частей она значит ничуть не меньше, чем другие.

Если бы я вдруг стал профессиональным художником (что очень маловероятно), я бы нарисовал математический анализ в образе суммы Римана.

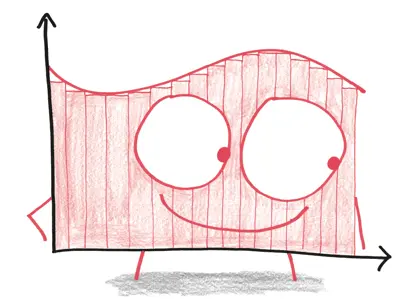
Роскошно, да, но перед нами не просто смазливая мордашка. Сумма Римана воплощает в себе сущность интеграла. Она носит имя Бернхарда Римана, застенчивого жителя Германии, одаренного богатым воображением. Он прожил всего 39 лет, но оставил свой след (и свои граффити-теги) во всех областях математики: Риманова поверхность, геометрия Римана, гипотеза Римана. В «Википедии» даже имеется страница под названием «Список объектов, названных в честь Бернхарда Римана». Там перечислены 70 пунктов, среди которых есть даже астероид и лунный кратер. «С каждым простым актом мышления, – писал Риман, – в нашу душу входит что-то постоянное и существенное».

Сумма Римана предлагает окончательное решение важной проблемы: что же представляет собой интеграл?

Один простой ответ на этот вопрос – «площадь, находящаяся под кривой». Достаточно справедливо. Но ты видишь где-то поблизости кривые, парень? Функции – это густонаселенные джунгли. Все треугольники, круги и трапеции, которые вы изучали в школе, были домашними мышками и кошками по сравнению со свирепыми зверями, которых вы найдете в непроходимых дебрях математики, с монстрами, которых никакая формула не может заключить в клетку.

Сумма Римана – это нечто вроде универсальной формулы, дротика с транквилизатором, который может успокоить любую функцию. Хотя действует она очень коварно, сама по себе идея чрезвычайно проста: добавляйте все больше, больше и больше прямоугольников.

Мы можем начать с четырех. Они стоят бок о бок, создавая линию горизонта из высотных зданий, их этажи направлены вниз к оси х , а крыши создают саму функцию. Если мы нарисуем график так, чтобы они находились внутри, то результат можно назвать «нижней суммой» – заниженной оценкой площади фигуры.

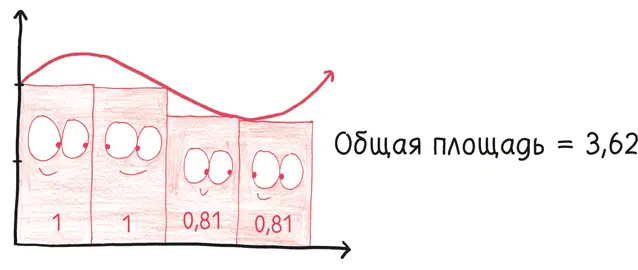
Теперь мы повторяем это упражнение, но на этот раз «потолки» прямоугольников не подпирают график функции, а лежат на нем, протыкая границы фигуры. Теперь мы немного переоцениваем реальную площадь, находя «верхнюю сумму».

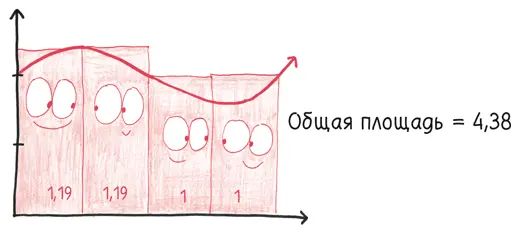
Это хорошая практика для любого действия по оценке, начиная с бюджета проекта и заканчивая угадыванием количества мармеладного драже в банке. До того как дать один ответ, вначале переоцените количество и недооцените его, сузив разброс возможностей между этими двумя пределами.

В любом случае в четырех прямоугольниках ничего особенного нет. Мы можем взять их 20 штук.

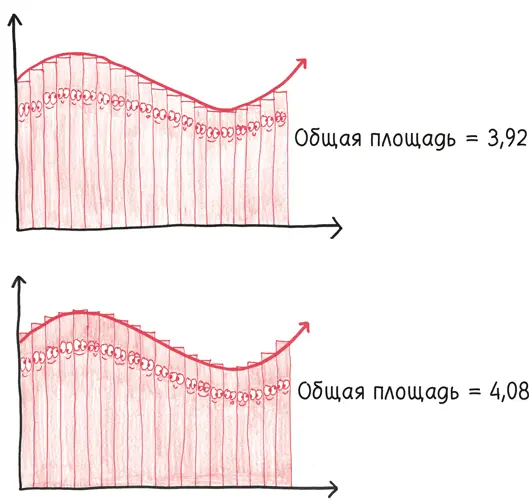
И тут «ловушка Римана» начинает удерживать зверя. Видите, как сокращается разрыв? Видите, как растет нижний потолок и падает верхний? Две суммы приближаются к единственной истине, и чем больше прямоугольников мы используем, тем ближе они сойдутся. Что насчет сотни прямоугольников, тысячи или миллиона? Что насчет миллиарда прямоугольников, квадриллиона или гугола? Что насчет бесконечного числа прямоугольников?