Бен Орлин - Время переменных. Математический анализ в безумном мире

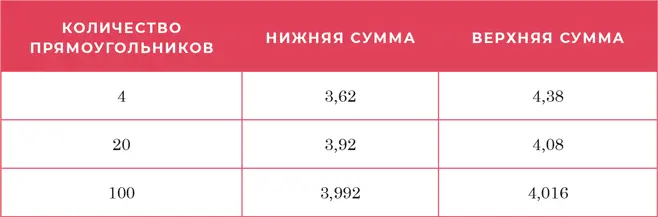
Теперь «ловушка Римана» захлопнулась. Мы отправляемся в воображаемое путешествие за грань возможного, где две оценки встретятся посередине, придя к одному значению – настоящая площадь, интеграл во всей красе.

Эта история объясняет смысл интеграла. Мы покрываем какую-то область бесчисленными крошечными прямоугольниками, каждый из которых имеет высоту y и ширину dx , то есть площадь y × dx . Последний штрих – это размашистый S-образный символ Лейбница, сжатая эмблема непрерывности и полноты, которая обозначает «сумму этого бесконечного множества вещей». (Забавный факт: в английском языке «интегральное исчисление» (integral calculus) – это анаграмма выражения «галантные завитки» (gallant curlicues).)

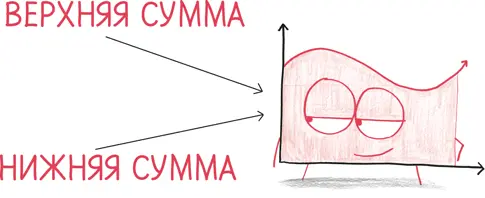
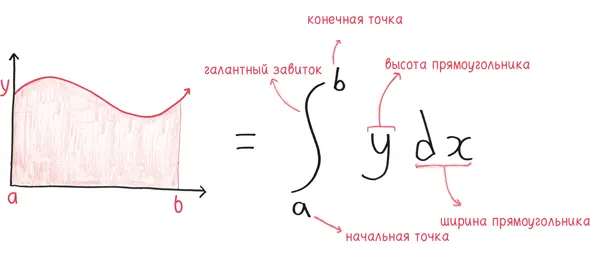
Хорошо, вот это и есть концепция интеграла Римана. «Но что насчет семиотики?» – спросите вы.

Хотя, возможно, вы не спросите. Возможно, никто никогда не спросит. Тем не менее разве сумма Римана не напоминает линию горизонта небоскребов Нью-Йорка? «Квадраты света следуют один за другим, уходят ввысь и теряются в ней», – писал о вечернем Нью-Йорке поэт Эзра Паунд. «Город взлетающей в высоту геометрии, – говорил эссеист Роланд Барт, – окаменевшая пустыня ячеек и решеток». Как и контур зданий на фоне неба, сумма Римана – это ансамбль, построенный из вертикальных линий.

Специалист по городскому дизайну Кристоф Линднер заметил, что «сопряженная геометрия этих форм… практически эксклюзивно выстраивает и определяет город с помощью вертикалей». (Тем временем писатель Генри Джеймс называл город «головокружительным» – словом, с которым вы могли бы смириться, если бы были Генри Джеймсом.) То же самое можно сказать и о сумме Римана: когда количество прямоугольников увеличивается, их ширина уменьшается, и мы имеем дело с объектом, направленным исключительно по вертикали.

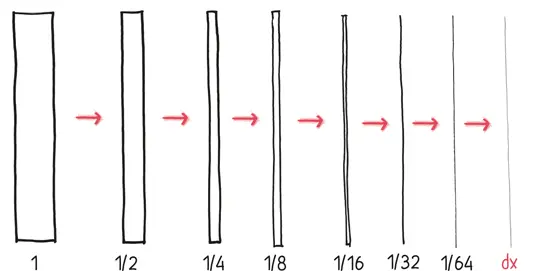
Некоторые считают, что линия горизонта в городе подражает природе и даже в чем-то превосходит ее. В романе «Источник» [44] Рэнд А. Источник. – М.: Альпина Паблишер, 2020. Айн Рэнд писала: «Я бы отдала самый прекрасный закат в мире за один взгляд на силуэты нью-йоркских небоскребов на фоне неба». «Этот архитектурный облик, – подхватывает литературный критик Морин Корриган, – мне милее, чем самый безмятежный закат или покрытые снегом вершины гор». Сумма Римана, как и контуры зданий, живет в таинственной долине. Ее упрощенная геометрия приближенно выражает перетекающую кривую, точно так же как силуэты зданий подражают природному пейзажу.

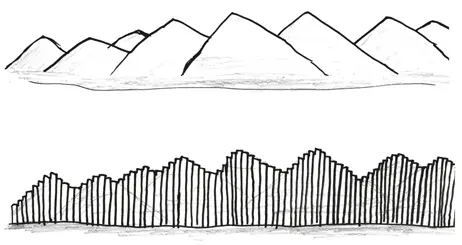
Риман преподнес свою теорию миру в 1854 г. А полвека спустя Анри Лебег разработал другую, и она оказалась лучше.

Чем же именно? Я просто ощущаю, как гневные плевки поклонников Римана и/или жителей Нью-Йорка летят в меня со всех сторон. Если оставаться справедливым, для большинства практических целей оба определения вполне эквивалентны. То, которое предложил Риман, спотыкается только в верхних слоях математического анализа, где атмосфера становится разреженной и абстрактной.

Возьмем печально известную функцию Дирихле. Вы вводите число. Если оно рациональное 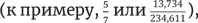на выходе получается единица; если число иррациональное (как √ –2 или π), на выходе – ноль.

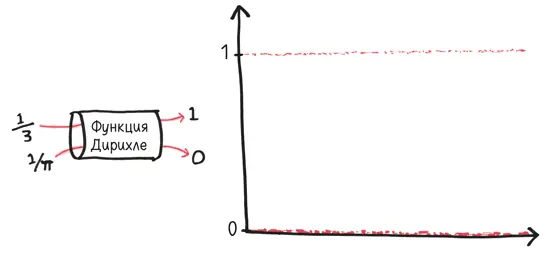
Теперь раскрою вам грязный секрет числовой оси – подавляющее большинство чисел являются иррациональными. Рациональные создают только тонкий слой пыли на том, что в своей основе есть иррациональный мир. (Возможно, это напомнит вам планету, на которой вы живете.) Таким образом, в правильном математическом смысле, интеграл этой функции, то есть площадь под этими частицами рациональной пыли, должен быть равен нулю. И именно об этом нам говорит интеграл Лебега.

Но интеграл Римана не может это обработать. Пыль загрязняет механизм, поэтому нижняя сумма всегда равна нулю, а верхняя сумма всегда остается единицей. Не важно, сколько прямоугольников вы используете, – эти две суммы никогда не сойдутся.

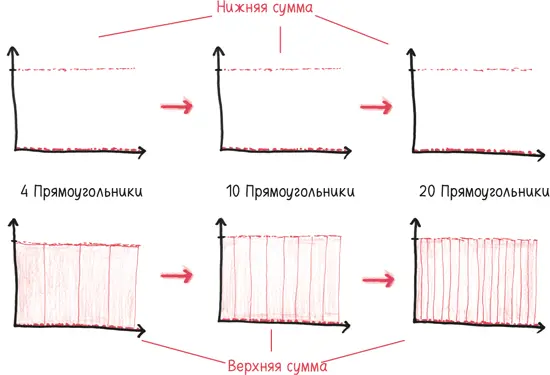
Мои скромные возможности не позволяют объяснить метод Лебега во всех подробностях, но я буду рад поделиться аналогией, которую он использовал. В письме к другу Лебег сравнивает свой интеграл и интеграл Римана с помощью образа человека, считающего свои деньги:

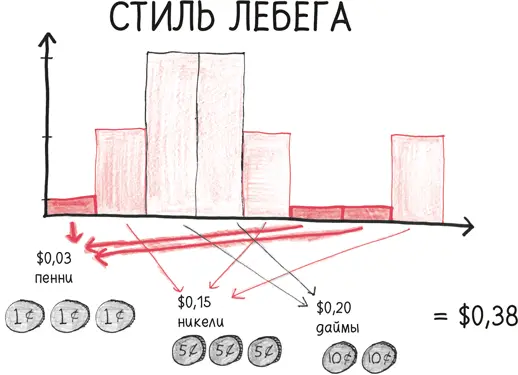
Я должен заплатить определенную сумму, которая лежит в моем кармане. Я достаю из него купюры и монеты и отдаю их кредитору в том порядке, в каком нахожу, пока не наберу всю сумму. Так действует интеграл Римана. Но я могу поступить по-другому. Достав из кармана все деньги, я раскладываю все купюры и монеты в соответствии с их стоимостью, а потом передаю одну за другой несколько кучек кредитору. Так работает мой интеграл.

Короче говоря, Риман пересчитывает купюры и монеты в том порядке, в котором они поступают.

Лебег, напротив, перераспределяет их, собирая пенни с пенни, никели с никелями, даймы с даймами [45] Пенни, никель, дайм – обиходные названия американских монет (1 цент, 5 центов, 10 центов). – Прим. науч. ред. .

Если вы находите, что интеграл – еще более неуловимое и расплывчатое понятие, чем производная, то не беспокойтесь. Так кажется не только вам. Производная получается с помощью бесконечного приближения, но интеграл на самом деле не связан с отдалением. Скорее он разрезает объект на бесконечное множество кусочков, перераспределяет их и вновь складывает, чтобы узнать что-то новое о целом.

А что же тогда с нашей метафорой о городских небоскребах? Если интеграл Римана – это линия горизонта с силуэтами домов, то чем же, черт побери, является интеграл Лебега?