Агниджо Банерджи - Эта странная математика. На краю бесконечности и за ним

Процессом удвоения точек аттрактора (от одной к двум, от двух к четырем и так далее), который мы наблюдали, когда значение k в нашем примере превысило 3, управляет важная математическая постоянная, называемая константой Фейгенбаума. Увидеть, как эта важная константа возникает, можно на этапах, предшествующих хаосу. Первая фаза, с циклом в одну точку, имеет длину 2, поскольку длится от k = 1 до k = 3. Вторая фаза, с циклом в две точки, имеет длину приблизительно 0,45, так как длится от k = 3 до k = 3,45. Отношение 2:0,45 равно примерно 4,45. Третья фаза имеет длительность около 0,095. Отношение 0,45: 0,095 приблизительно равно 4,74. И так далее. Эти отношения стремятся к константе Фейгенбаума, которая приблизительно равна 4,669. Длительность фаз сокращается экспоненциально, так что к моменту, когда k достигает 3,57, цикл повторяется бесконечное количество раз.

Константа Фейгенбаума выявляется в результате процесса, который мы только что рассмотрели, но ее фундаментальность для теории хаоса в том, что она обнаруживается во всех аналогичных хаотических системах. Какое уравнение ни возьми (если только оно отвечает определенным базовым условиям), оно будет иметь циклы, длина которых изменяется вдвое в соответствии с константой Фейгенбаума.

Чтобы увидеть, как хаотические процессы приводят к образованию фракталов, можно взять тот же итеративный процесс и нанести на сетку координат аттракторы для каждого значения k . Бо́льшая часть из того, что появляется после k = 3,57, – чистый хаос, но есть несколько значений k , для которых существует конечный аттрактор. Их называют “островами стабильности”. Один из таких островов образуется при значении k , близком к 3,82. В этом месте мы обнаруживаем аттрактор, состоящий всего из трех значений. Приблизив на графике любое из этих значений, мы видим рисунок, очень похожий на весь график в целом, хоть и не повторяющий его в точности.

В ходе своих новаторских исследований хаоса Лоренц также обнаружил новый вид фрактала, так называемый странный аттрактор. Обычный аттрактор прост в том смысле, что точки стремятся к нему, а затем совершают определенные постоянные циклы в его окрестностях. Странные же аттракторы, как мы увидим, ведут себя иначе. Для того чтобы получить первый пример странного аттрактора, Лоренц использовал систему дифференциальных уравнений. При увеличении масштаба в любой его точке появлялось бесконечное множество параллельных линий. Любая точка на аттракторе передвигалась по хаотической траектории рядом с ним, никогда не возвращаясь точно в исходное положение, а две точки, находившиеся изначально очень близко друг к другу, быстро расходились и в итоге оказывались на совершенно разных траекториях. Чтобы провести аналогию с физическим миром, представьте себе шарик для настольного тенниса и океан. Если шарик сбросить с высоты над океаном, он будет быстро падать, пока не коснется воды. Если его погрузить под воду и отпустить там, он быстро всплывет. Но как только он оказывается на поверхности океана, его движение становится совершенно непредсказуемым и хаотичным. Точно так же точка, не находящаяся на странном аттракторе, будет стремительно двигаться по направлению к нему. Достигнув же странного аттрактора, она начинает двигаться вблизи него хаотично.

Изучение фракталов – увлекательнейшее занятие, а по красоте мало какой математический объект способен составить им конкуренцию. Но кроме того, они играют важнейшую роль в физическом мире. В основе любого природного явления, которое кажется нам случайным и неупорядоченным, может лежать фрактал. Более того, можно даже утверждать, что все объекты и явления, существующие в этом мире, – фракталы, поскольку все они на любом уровне имеют ту или иную структуру, по крайней мере до уровня атомов. Облака, вены на руке, разветвления бронхов, листья деревьев – все они имеют структуру фрактала. В космологии по фрактальному принципу распределяется материя по Вселенной, и фрактал этот имеет структуру даже на уровнях меньше атомного ядра, вплоть до предельного значения расстояния, которому присвоен физический смысл, – так называемой планковской длины, равной 1,6 × 10 –35метра, или приблизительно одной стоквинтиллионной размера протона.

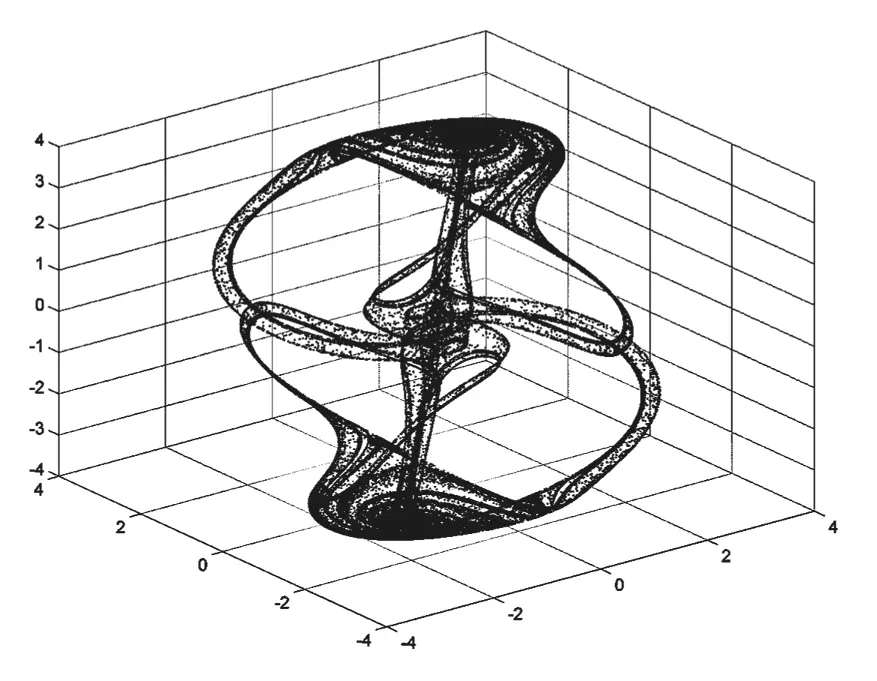
Странный аттрактор, известный как “циклически симметричный аттрактор Томаса”.

Фракталы существуют не только как пространственные узоры, но и как временны́е. Возьмите игру на ударных: можно легко запрограммировать компьютер на создание и воспроизведение барабанной партии или посадить за ударную установку музыканта-робота. Но в игре профессиональных барабанщиков есть нечто, что отличает ее от идеально размеренного, безукоризненно точного ритма, производимого их электронными коллегами. И это “нечто” – незначительные изменения ритма и громкости, едва заметные отклонения от совершенства, которые, как показывают исследования, имеют фрактальный характер.

Международная группа ученых проанализировала работу на ударных Джеффа Поркаро, участника группы Toto , прославившегося своей виртуозной игрой на хай-хэте (сдвоенных тарелках), на котором он играл одной рукой. Как в ритме, так и в громкости ударов по хай-хэту исследователи обнаружили самоподобные фигуры, общая структура которых перекликалась с рисунком более коротких пассажей. Игра Поркаро на ударных – это акустический эквивалент фрактальной береговой линии, проявляющий самоподобие при различных масштабах. Кроме того, ученые установили, что слушателям больше нравятся именно такого рода вариации, а не идеально выстроенный ритмический рисунок или, наоборот, более случайный.

Фрактальные фигуры у каждого барабанщика свои, и это одна из особенностей, которая делает их игру уникальной и узнаваемой. Похожее наблюдается и у музыкантов, играющих на других инструментах. Эти мельчайшие отклонения от идеала – то, что отличает человека от машины.

Поскольку вокруг нас так много фракталов (пусть и не в строгом математическом смысле этого термина), компьютер способен быстро создать изображение, очень похожее на реальный объект, например, нарисовать дерево. Дайте ему лишь формулу и начальные данные – и через мгновение он выдаст вам фантастически реалистичную картинку. Неудивительно, что эта техника быстрого создания моделей планет, облаков, движущейся воды, ландшафтов, скал, растений и других объектов пейзажа так полюбилась специалистам по анимации и по компьютерной графике в кино, разработчикам авиасимуляторов и компьютерных игр. Нет нужды держать огромную базу данных со всеми объектами и локациями, необходимыми для съемки реалистичной сцены, – ведь компьютер запросто просчитает и построит все с лету, всего лишь повторяя на высокой скорости несколько несложных операций. Этот перспективный подход может сыграть важную роль в разработке будущих технологий погружения, в частности виртуальной реальности, где целью является создание действующих в реальном времени трехмерных изображений, неотличимых от окружающих нас объектов и явлений.