Дэвид Шпигельхалтер - Искусство статистики. Как находить ответы в данных

Хотя это не самый насущный научный вопрос, который я исследовал, когда преподавал в Африканском институте математических наук [187]в 2013 году, он был прекрасным упражнением для аудитории, а мне действительно хотелось узнать ответ [188]. Я получил данные по 54 аспирантам со всей Африки. Табл. 10.1 показывает общее распределение ответов по полу и положению правой или левой руки сверху. Такой тип таблицы в статистике называется таблицей сопряженности, или факторной таблицей.

Таблица 10.1

Таблица сопряженности полов и положения рук при скрещивании для 54 аспирантов

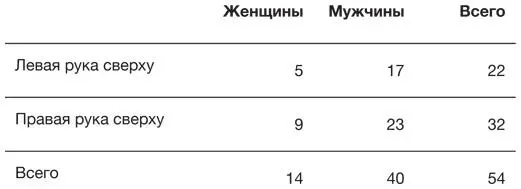
В целом большинство кладут сверху правую руку (32/54 = 59 %). Однако у женщин доля таких «праворуких» (9/14 = 64 %) выше, чем у мужчин (23/40 = 57 %): наблюдаемая разница между долями составляет 64–57 = 7 %. В этом случае нулевая гипотеза состоит в том, что между скрещиванием рук и полом нет никакой связи, а потому наблюдаемая разница в долях между полами должна равняться 0 %. Ключевой вопрос: может ли наблюдаемое отклонение в 7 % считаться достаточно большим, чтобы противостоять нулевой гипотезе?

Чтобы ответить на этот вопрос, нужно знать, какой разницы в долях мы можем ожидать просто вследствие случайного разброса при справедливости нулевой гипотезы, то есть независимости скрещивания рук и пола. Более формально: совместима ли наблюдаемая разница 7 % с нулевой гипотезой? [189]

Это сложная, но важная идея. Когда Арбетнот проверял свою нулевую гипотезу, согласно которой мальчики и девочки рождаются равновероятно, он смог легко выяснить, что наблюдаемые данные ни в малейшей степени не совместимы с нулевой гипотезой – шансы, что по чистой случайности мальчики будут численно превосходить девочек 82 года подряд, ничтожно малы. В более сложных ситуациях выяснить, совместимы ли данные с нулевой гипотезой, не так просто. Однако приведенный ниже тест перестановкиотображает мощную процедуру, позволяющую избежать сложной математики.

Представьте, что все 54 человека выстроились в ряд, сначала 14 женщин, а затем 40 мужчин, и каждому присвоен номер от 1 до 54. Допустим, у каждого есть билет, указывающий, какая рука у него при скрещивании сверху – левая или правая. А теперь вообразите, что все эти билеты смешали в шляпе и раздали присутствующим наугад. Это пример того, каких результатов можно ожидать, если бы нулевая гипотеза была верна, ведь при случайной раздаче скрещивание рук и пол никак не связаны.

Но даже при случайном распределении доля «держащих сверху правую руку» не будет в точности совпадать для мужчин и женщин (просто из-за чистой случайности), и мы можем вычислить наблюдаемую разницу в долях для этой случайной раздачи билетов. Затем мы могли бы повторить процесс, скажем 1000 раз, и посмотреть, какое распределение будет у этой разницы. Результаты приведены на рис. 10.2(a): показан разброс наблюдаемых разниц – некоторые в пользу мужчин, некоторые в пользу женщин – с центром в нуле. Фактически наблюдаемая разница находится недалеко от центра распределения.

Рис. 10.2

Эмпирическое распределение разницы между долями женщин и мужчин, которые при скрещивании рук кладут сверху правую руку: (a) для 1000 случайных перестановок, (b) для всех равновероятно возможных перестановок по отношению к скрещиванию рук. Наблюдаемое различие в пропорциях (7 %) обозначено вертикальной пунктирной линией

В качестве альтернативы (при наличии времени) можно взять все возможные перестановки билетов, не ограничиваясь моделированием 1000 симуляций. Каждая перестановка даст какую-то наблюдаемую разницу в долях «праворуких» у мужчин и женщин, и, нанеся на график все результаты, мы получим более гладкое распределение, чем построенное по 1000 симуляциям.

К несчастью, таких перестановок масса, и даже если вычислять их со скоростью миллион в секунду, на это уйдет число лет с 57 нулями [190]. К счастью, нам незачем производить эти вычисления, поскольку распределение для наблюдаемой разницы в таких долях при нулевой гипотезе можно найти теоретически: оно представлено на рис. 10.2(b) и основано на так называемом гипергеометрическом распределении.

Рис. 10.2 показывает, что реально наблюдаемая разница в долях «праворуких» мужчин и женщин (7 % в пользу женщин) лежит достаточно близко к центру распределения для разниц, которых можно было бы ожидать, если бы никакой связи вообще не было. Нам нужна мера, характеризующая, насколько близко к центру лежит наблюдаемое значение, и одна из таких характеристик – это площадь хвоста распределения. Например, площадь части фигуры, расположенной справа от вертикальной пунктирной линии, составляет 0,45, или 45 %.

Это число именуется P-значением [191]и считается одним из самых полезных понятий в статистике, а потому заслуживает строгого определения: P-значение – это вероятность получить результат, по крайней мере такой же или более экстремальный, чем наблюдаемый, если нулевая гипотеза (и все другие предположения моделирования) на самом деле верна.

Но тут есть важный нюанс, что мы подразумеваем под «экстремальным» результатом? Наше P-значение 0,45 одностороннее, так как указывает, насколько вероятно получить в эксперименте не меньшую разницу в пользу только женщин, если нулевая гипотеза верна. Это P-значение используется при так называемых односторонних критериях. Но ведь большая разница в пользу мужчин тоже заставила бы нас сомневаться в справедливости нулевой гипотезы. Поэтому мы должны также вычислить вероятность получить отклонение не меньше 7 % в обоих направлениях. Так появляются двусторонниеP-значения, соответствующие двусторонним критериям. Общая площадь двух частей фигуры, отдаленных от центра-нуля больше чем на 7 %, равна примерно 0,89, а поскольку это значение близко к единице, следовательно, наблюдаемое значение находится близко к центру нулевого распределения. Конечно, на рис. 10.2это видно и так, но, учитывая, что подобные гистограммы доступны не всегда, нам нужно число, формально выражающее «экстремальность» наших данных.

Арбетнот предоставил первый зафиксированный пример такой процедуры: при нулевой гипотезе (когда девочки и мальчики рождаются с равной вероятностью) вероятность того, что 82 года подряд мальчики будут рождаться чаще девочек, равна 1/2 82. Но так определяется «экстремальность» только в терминах превосходства мальчиков. А поскольку мы можем сомневаться и в нулевой гипотезе, что 82 года подряд девочки будут рождаться чаще мальчиков, то должны удвоить это число, чтобы получить экстремальный результат в обоих направлениях. Поэтому число 1/2 82можно считать первым установленным двусторонним P-значением, хотя этот термин появился только через 250 лет.