Дэвид Шпигельхалтер - Искусство статистики. Как находить ответы в данных

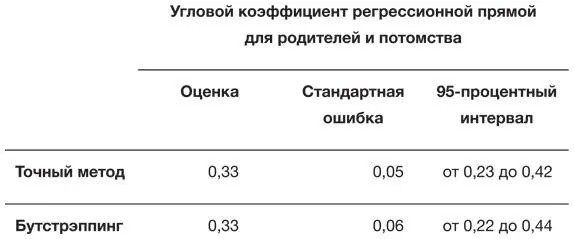
В главе 7мы узнали, как с помощью бутстрэппинга получить 95-процентные интервалы для углового коэффициента регрессионной прямой, связывающей рост матерей и дочерей. Гораздо проще получить точные интервалы, основанные на теории вероятностей и включенные в стандартные программы. Табл. 9.1 показывает, что они дают весьма сходные результаты. «Точные» интервалы, основанные на теории вероятностей, требуют больше предположений, чем метод бутстрэппинга, и, строго говоря, будут точными только в случае нормального распределения. Но центральная предельная теорема говорит, что при настолько большом объеме выборки разумно считать, что наши оценки имеют нормальное распределение, поэтому такие интервалы приемлемы.

Таблица 9.1

Оценки коэффициента регрессионной прямой, демонстрирующей связь между ростом дочерей и матерей. Стандартные ошибки и 95-процентные интервалы точные и для бутстрэппинга, основанного на 1000 перевыборок

Традиционно используются 95-процентные интервалы, которые обычно отклоняются от среднего на две стандартные ошибки в обе стороны [179]; однако иногда интервалы берутся у же (например, 80 %) или шире (99 %). Статистическое управление США использует для определения уровня безработицы 90-процентные интервалы, в то время как Национальное статистическое управление Великобритании – 95 %. Важно уточнять, какой именно интервал используется.

Погрешности опросов

Когда какое-то заявление базируется на опросе (например, опросе общественного мнения), стандартная практика – указать статистическую погрешность. У статистики безработицы, приведенной в главе 7, на удивление большая погрешность (оценка в 3000 имеет погрешность ±77 000). Это значительно влияет на интерпретацию исходного числа – в нашем случае такая погрешность показывает, что мы даже не знаем, выросла безработица или сократилась.

Существует простое эмпирическое правило: если вы оцениваете процент людей, предпочитающих, скажем, на завтрак чай, а не кофе, и рассматриваете случайную выборку из генеральной совокупности, то ваша погрешность (в процентах) будет максимум плюс-минус 100, деленное на квадратный корень из размера выборки [180]. Поэтому при выборке в 1000 человек (стандартный объем в таких опросах) погрешность обычно указывается как ±3 % [181]. Если 400 человек предпочитают кофе, а 600 – чай, то вы можете примерно оценить реальную долю любителей утреннего кофе в популяции следующим образом: 40 ±3 %, то есть от 37 до 43 %.

Конечно, это верно только в случае, если устроители опроса действительно взяли случайную выборку, а все респонденты ответили, причем правду. Таким образом, хотя мы и можем вычислить погрешность, мы должны помнить, что вычисления верны, если примерно верны и наши предположения. Но можем ли мы на них опираться?

Можно ли доверять погрешностям?

Перед всеобщими выборами в Соединенном Королевстве в июне 2017 года публиковались многочисленные опросы общественного мнения с участием в каждом примерно 1000 респондентов. Если бы это были идеально случайные опросы, где участники давали бы правдивые ответы, то максимальная погрешность составила бы ±3 % и разброс результатов опросов относительно их среднего значения находился бы в этом диапазоне, поскольку предполагалось, что выборка каждый раз берется из одной и той же генеральной совокупности. Однако рис. 9.3, основанный на диаграмме, использованной «Би-би-си», показывает, что рассеяние было намного больше. А значит, погрешности не могли быть верными.

Рис. 9.3

Способ визуализации данных социологических опросов, проведенных «Би-би-си» перед всеобщими выборами в Великобритании 2017 года [182]. Линия тренда – это медиана предыдущих семи опросов. В каждом опросе, как правило, участвовали 1000 человек, поэтому максимальная погрешность предполагалась ±3 %. Однако разбросы у разных опросов значительно превосходят эту величину. Данные приведены только для двух партий – Консервативной и Лейбористской

Мы уже знаем много причин, почему опросы бывают неточными, не считая неизбежной (поддающейся количественному определению) погрешности из-за случайного разброса. В этом случае вину за излишнее рассеяние можно возложить на методы составления выборки, в частности на телефонные (причем в основном с использованием стационарных телефонов) опросы с очень низким коэффициентом ответов, вероятно, от 10 до 20 %. Я лично придерживаюсь эвристического правила, что для учета допущенных в опросе систематических ошибок заявленную погрешность нужно удвоить.

Мы не можем ожидать полной точности от предвыборных опросов, но могли бы ожидать большего от ученых, занимающихся измерением физических констант, например скорости света. Однако долгая история заявляемых погрешностей в таких экспериментах впоследствии оказалась безнадежно подпорченной: в первой половине XX века интервалы неопределенности вокруг оценок скорости света не включали значение, принятое сейчас.

В результате организациям, занимающимся метрологией (наукой об измерениях), пришлось указать, что погрешности всегда должны базироваться на двух компонентах:

• Тип А: стандартные статистические показатели, обсуждаемые в этой главе, которые при увеличении числа измерений предположительно станут снижаться.

• Тип В: систематические ошибки, которые, как ожидается, не уменьшатся при увеличении числа наблюдений и должны обрабатываться с использованием нестатистических средств, таких как экспертные суждения или внешние свидетельства.

Эти идеи должны пробудить в нас некоторое смирение в отношении статистических методов, которые мы можем применить к отдельному источнику данных. При наличии фундаментальных проблем со способом сбора данных никакие умные методы не помогут устранить такие ошибки, и нам нужно использовать знания и опыт, чтобы скорректировать свои заключения.

Что происходит, когда у нас есть все возможные данные?

Вполне естественно использовать теорию вероятностей для определения погрешностей в результатах опроса, поскольку его участники рандомно выбираются из более крупной совокупности, поэтому понятно, как в генерирование данных проникает случайность. Но давайте снова зададимся вопросом: а если наши статистические данные полные, то есть учитывают все, что произошло? Например, ежегодно некая страна учитывает все убийства. Если предположить, что в подсчетах нет ошибок (и согласовать определение термина «убийство»), то это будет просто описательная статистика без погрешностей.