Владимир Арнольд - Теория катастроф

Рис. 56. Диссипация энергии в яме и у барьера

Причина, по которой сложенные особенности встречаются столь часто, состоит в том, что часто встречаются как обычные особенности векторного поля, так и складывания. Неожиданным здесь является лишь то, что комбинирование складывания с особенностью не приводит к большему разнообразию случаев, чем в классификации самих особенностей векторных полей. А именно, рассмотрим складывание как инволюцию (диффеоморфизм, квадрат которого — тождественное преобразование) на плоскости, несущей векторное поле с особой точкой. Если линия неподвижных точек инволюции проходит через особую точку поля и инволюция на этой линии меняет знак каждого вектора поля на противоположный, то такая инволюция (почти всегда) переводится в любую другую инволюцию с такими свойствами при помощи диффеоморфизма, двигающего вдоль себя каждую фазовую кривую заданного поля. Этот (довольно неожиданный) результат является источником всей описанной выше теории.

Четвертая особенность границы достижимости получается из двух сепаратрис сложенных седел, входящих с разных сторон в сложенный узел. Приведенная выше нормальная форма сложенного узла позволяет явно выписать нормальную форму четвертой особенности, но я здесь не буду этого делать.

Примеры управляемых систем и целей, приводящих к указанным особенностям границы достижимости, изображены на рис. 57, 58, 59. На этих рисунках цель у обозначена двойной линией, граница области достижимости — Т-образным пунктиром (ножка буквы Т обращена в сторону области достижимости). Линии со стрелками касаются краев конусов допустимых направлений в каждой точке; горизонтально заштрихована область "полной управляемости, (выпуклая оболочка индикатрисы окружает 0). Рассматривая рис. 57 — 59 читатель может проверить неустранимость особенностей 1 — 4.

Чтобы разобраться в этих рисунках, мы построим сеть предельных линий , определяемую следующим образом.

В каждой точке вне области полной управляемости направления допустимых скоростей расположены внутри угла, меньшего 180°.

Стороны этого угла определяют направления предельных скоростей в данной точке. Таким образом, в каждой точке вне области полной управляемости возникают два предельных направления. Интегральные кривые нолей предельных направлений (т. е. кривые, имеющие предельное направление в каждой своей точке) называются предельными линиями .

Сеть предельных линий изображена на рис. 54 вместе с индикатрисами допустимых скоростей (они имеют вид эллипсов) и с опирающимися на индикатрисы углами, образованными допустимыми направлениями движения.

Граница области достижимости состоит из отрезков предельных линий (и, быть может, отрезков линии цели, если цель не лежит в области полной управляемости, см. рис. 57). Эти отрезки соединяются между собой в точках, которые и составляют особенности границы области достижимости.

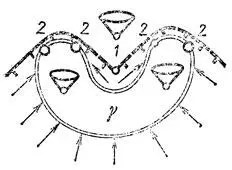
Рис. 57. Устойчивость особенностей 1 и 2 на границе области достижимости

На рис. 57 цель имеет вид контура лежащей на спине буквы С. допустимые скорости во всех точках плоскости одинаковы и надавлены вверх под углом, составляющим не более 45° с вертикалью.

Наклон всех предельных линий ±45°. Граница достижимости обозначена Т-образным пунктиром. Видны особые точки границы двух типов: 1 и 2.

В точке 1 соединяются отрезка двух разных предельных линий . Они пересекаются под ненулевым углом. Ясно, что из точек, расположенных выше указанной на рис. 57 границы, при движении по направлению, образующему с вертикалью угол 45° или меньше, попасть на цель нельзя, а из точек, расположенных ниже, — можно. Интересно отметить, что вершина 1 зияет на границе области достижимости: область недостижимости вклинивается в этом месте в области достижимости. Таким образом, в смысле п. 7 хороший оказывается именно недостижимое.

В точке 2 на границе достижимости соединяется отрезок предельной линии и отрезок линии-цели . В этой точке направление линии-цели предельное, так что граница достижимости имеет касательную. Кривизна границы, однако, меняется в точке 2 скачком при переходе с предельной линии на линию-цель.

Заменим теперь цель на рис. 57 любой близкой гладкой кривой (близость кривых предполагает близость их касательных, кривизн и т. д.) и заменим поле индикатрис допустимых скоростей на рис. 57 близким полем. Тогда ясно, что граница допустимости новой системы по-прежнему будет иметь вблизи точки 1 точку излома (где под ненулевым углом соединяются отрезки двух предельных линий). Точно так же вблизи каждой из точек 2 возникает точка аналогичного характера для новой системы.

Таким образом, ситуация, изображенная на рис. 57, устойчива относительно малых шевелений системы. Подобным свойством устойчивости обладают и ситуации, изображенные на рис. 58 и 59. События, приводящие к указанным на этих рисунках особенностям сети предельных линий, состоят в следующем.

На рис. 58 кривая К ограничивает заштрихованную область полной управляемости: в заштрихованной области движение в любом направлении возможно (если допускать так называемые смешанные стратегии, т. е. движения быстро сменяющимися галсами). Цель на рис. 58 лежит в области полной управляемости. Следовательно, вся ограниченная кривой К область достижима.

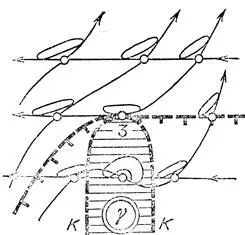
Рис. 58. Устойчивость особенности 3 на границе области достижимости

На границе К области полной управляемости угол между допустимыми направлениями составляет ровно 180°. Граница К образована теми точками плоскости, для которых двойная касательная, делающая выпуклой индикатрису допустимых скоростей, проходит через начало координат плоскости скоростей (двойная касательная — это прямая, касающаяся кривой в двух точках).

На рис. 58 эта двойная касательная в каждой точке кривой К горизонтальна. Событие, приводящее к образованию изображенной на рис. 58 особенности, состоит в том, что кривая К сама касается проходящей через пуль двойной касательной к индикатрисе .

Для систем общего положения такое событие происходит лишь в отдельных точках границы К области полной управляемости. На рис. 58 оно происходит в точке 3, где касательная к К горизонтальна.

Из сказанного выше ясно, что описанное событие реализуется устойчивым образом: при малом шевелении системы, т. е. цели и поля индикатрис допустимых скоростей, точка 3 несколько сместится, но не исчезнет.

Рассмотрим теперь сеть предельных линий вблизи точки 3. Оба поля предельных направлений вблизи нее гладкие. Выбором соответствующей системы координат одно из них можно выпрямить. На рис. 58 система координат так и выбрана: первое из двух семейств предельных линий состоит из горизонтальных прямых (направленных влево).