Владимир Арнольд - Теория катастроф

Зависимость кратчайшего времени достижения цели от начальной точки может иметь особенности. Рассматривавшиеся в н. 10 особенности функции минимума расстояния до кривой — частный случай (индикатриса — окружность, а цель — кривая). В отличие от этого частного случая особенности кратчайшего времени в общей задаче управления изучены весьма слабо.

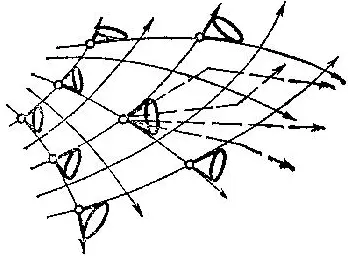
Рис. 54. Поле индикатрис допустимых скоростей управляемой системы

В общем случае достичь цели можно не при любом начальном условии. Точки фазового пространству из которых можно достичь цели (за любое время), называются областью достижимости .

Граница области достижимости может иметь особенности даже в том случае, когда пи цель, ни поле индикатрис в различных точках фазового пространства особенностей не имеют. Мы приводим ниже классификацию особенностей границы достижимости в общей управляемой системе па фазовой плоскости в случае, когда индикатрисы и цель — гладкие кривые (по А. А. Давыдову).

Из четырех типов особенностей границы три записываются простыми формулами (при подходящем выборе локальных координат на плоскости):

1) у = |х|, 2) у = х|х|, 3) у = х 2|х|.

Особенность четвертого тина связана с теорией дифференциальных уравнений, неразрешенных относительно производной, называемых также неявными дифференциальными уравнениями.

Такое уравнение имеет вид F(х, у, р) = 0, где р = dy/dx. Геометрически уравнение F = 0 задает поверхность в трехмерном пространстве с координатами (х, у, р). Она называется поверхностью уравнения .

Условие р = dy/dx выделяет плоскость в каждой точке нашего трехмерного пространства. Эта плоскость состоит из векторов, у-компонента которых в р раз больше х-компоненты, где р — координата точки приложения. Такая плоскость называется контактной. Контактная плоскость в каждой точке вертикальна (содержит направление оси р). Все вместе контактные плоскости задают поле контактных плоскостей, называемое также контактной структурой.

Контактная структура высекает на поверхности уравнения поле направлений (с особыми точками в тех местах, где контактная плоскость касается поверхности). Поверхность уравнения здесь предполагается гладкой. Это условие выполняется для уравнений общего положения.

Вопрос о строении типичных особых точек неявных дифференциальных уравнений рассматривался еще в прошлом веке, и король Швеции Оскар II включил его, наряду с проблемой трех тел, а список из четырех вопросов на премию 1885 г.

Решение этого вопроса было получено лишь в 1985 г. А. А. Давыдовым в виде побочного продукта исследования областей достижимости управляемых систем па плоскости.

Ответ доставляет следующий список нормальных форм (к которым уравнение приводится локальным диффеоморфизмом плоскости):

У = (х + kр) 2.

В зависимости от значения параметра к здесь возможны три случая. Особая точка поля на поверхности уравнения может оказаться седлом, узлом или фокусом. Отображение проектирования поверхности уравнения на плоскость (х, у) вдоль оси р имеет особенностью складку. В окрестности типичной точки складки уравнение приводится к нормальной форме Чибрарио (1932), х = р 2. Все особые точки автоматически попадают на складку. Результат складывания изображен на рис. 55: особые точки па плоскости (х, у) называются сложенным седлом ( узлом, фокусом соответственно). Оказывается, несмотря па сложность узора, образованного интегральными кривыми па плоскости (х, у), он (даже не только топологически, но и с точностью до диффеоморфизма) однозначно определяется единственным "модулем" k (как и фазовый портрет соответствующего векторного поля на плоскости вблизи особой точки).

Сложенные особые точки — седла, узлы, фокусы — встречаются во многих приложениях. Рассмотрим, например, асимптотические линии на поверхности в трехмерном пространство (поверхность имеет с касательными прямыми касание выше первого порядка в каждой своей точке). Для поверхности общего положения сеть асимптотических линий заполняет область гиперболичности, где поверхность имеет отрицательную кривизну (как обыкновенное седло). Через каждую точку области гиперболичности проходят две асимптотические лини и область гиперболичности ограничена линией параболических точек, на которой оба асимптотических направления совпадают.

В окрестности типичной параболической точки асимптотические линии имеют полу кубическую особенность и вся сеть их приводится к такой же нормальной форме у = с ± х 3/2как и семейство интегральных кривых уравнения Чибрарио.

Однако в окрестности отдельных точек на линии параболичности поведение асимптотических линий сложнее: они устроены как интегральные кривые неявных уравнений вблизи сложенных особых точек (рис. 55).

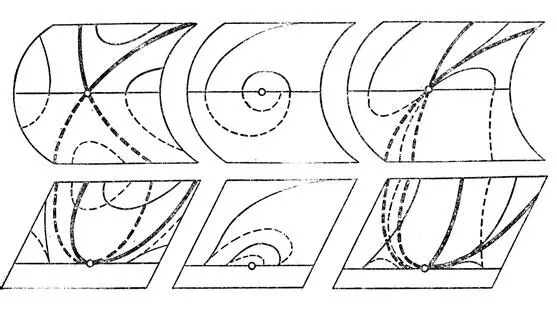
Рис. 55. Сложенные особенности

Сложенные особенности появляются также в теории релаксационных колебаний. Пусть система имеет одну быструю и две медленных переменных, так что полное фазовое пространство трехмерно. Точки, где скорость изменения быстрой переменной равна нулю, образуют (вообще говоря гладкую) поверхность — медленную поверхность системы. Движение фазовой точки состоит из нескольких процессов. Вначале быстрая переменная релаксирует , т. е. фазовая точка быстро движется по "вертикали" (по направлению оси быстрой переменной) к медленной поверхности, затем начинается медленное движение вдоль этой поверхности. Траектории этого движения определяются полем направлений, высекаемым на ней полем плоскостей, натянутых на вертикальное направление (направление оси быстрой переменной) и направление возмущений. Это поле плоскостей определяет, вообще говоря, контактную структуру в фазовом пространстве, и особенности медленного движения описываются, вообще говоря, сложенными особыми точками рис. 55.

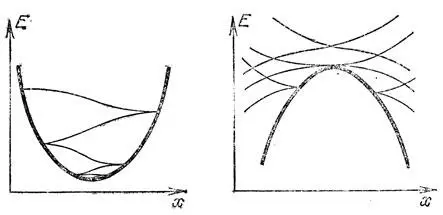
В качестве последнего примера тех же особенностей рассмотрим движение материальной точки в потенциальной яме (или у потенциального барьера) в присутствии трения. Обозначим (рис. 56) через х координату точки, а через Е ее полную энергию. Проекции фазовой траектории на плоскость (х, Е) имеют при подходе к графику потенциальной энергии полукубические, вообще говоря, особенности. Минимуму (максимуму) потенциальной энергии отвечает особая точка. Для потенциальной энергии общего положения получаются все те же сложенные особенности Давыдова.