Владимир Арнольд - Теория катастроф

Например, метаморфоза волнового фронта 5 на рис. 36 соответствует ласточкину хвосту на каустике. Ребро возврата движущегося в трехмерном пространстве волнового фронта заметает поверхность каустики (ласточкин хвост). Однако это разбиение каустики на кривые — не то разбиение поверхности ласточкиного хвоста на плоские кривые, с которым мы встречались выше (на рис. 35). Ребро возврата движущегося фронта не имеет самопересечений. Через точку линии самопересечения каустики ребро возврата движущегося фронта проходит два раза. Интервал времени между этими прохождениями очень мал (порядка ε 5/2, где ε — расстояние от вершины хвоста).

Точно так же при перестройках 3 и 4 (см. рис. 36) ребра возврата движущихся фронтов заметают пирамиду и кошелек.

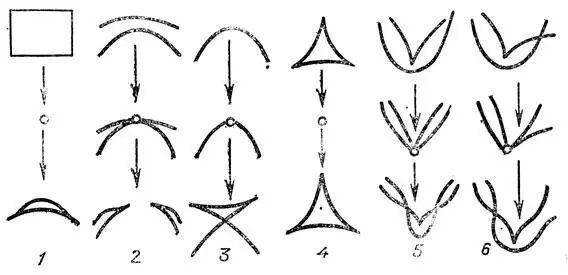
Рис. 40. Типичные перестройки каустик на плоскости

Если исходный фронт движется (зависит от параметра), то его каустика также движется и при своем движении способна испытывать метаморфозы. Метаморфозы движущихся каустик на плоскости можно изучить, рассматривая сечения большой каустики в пространстве-времени , подобно тому, как мы это делали для фронтов. Полученные метаморфозы изображены на рис. 40. (Это метаморфозы плоских сечений ласточкиного хвоста, кошелька и пирамиды.) Все более сложные метаморфозы рассыпаются на последовательности перечисленных при малом шевелении однопараметрического семейства.

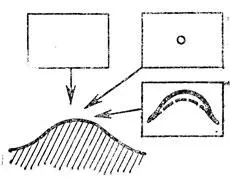
Рис. 41. Перестройка 'губы': рождение видимого контура

Обратим внимание па метаморфозу 1 рождения каустики "из воздуха", Новорожденная каустика имеет вид серпика с полукубическими остриями на концах (" губы ", но терминологии Р. Тома). Аналогичным образом рождается "из воздуха" видимый контур поверхности при изменении направления проектирования (рис. 41), Глядя на бугор сверху, мы не видим контура. Когда луч зрения наклоняется, появляется вначале точечная особенность, которая затем быстро растет (пропорционально √t — t 0, где t 0— момент появления особенности) и имеет вид "губ". Описанную здесь перестройку можно реализовать как перестройку плоского сечения поверхности с ребром возврата при поступательном движении плоскости (в момент перестройки плоскость касается ребра возврата (рис. 42)).

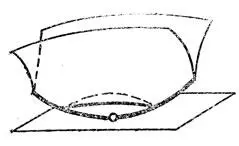
Рис. 42. Перестройка плоского сечения поверхности с ребром возврата

Метаморфозу 3 также можно увидеть на видимом контуре, для этого достаточно посмотреть на двугорбого верблюда, проходя мимо него (рис. 43). В момент метаморфозы профиль имеет такую же особенность, как кривая у 3= х 4.

Рис. 43. Перестройка 'верблюд'

Все перестройки видимых контуров поверхностей в общих однопараметрических семействах исчерпываются первыми тремя изображенными на рис. 40, 1 — 3.

Метаморфозы каустик, движущихся в трехмерном пространстве , получаются сечениями больших (трехмерных) каустик в четырехмерном пространстве-времени трехмерными изохронами, Эти метаморфозы изображены на рис. 44 и 45.

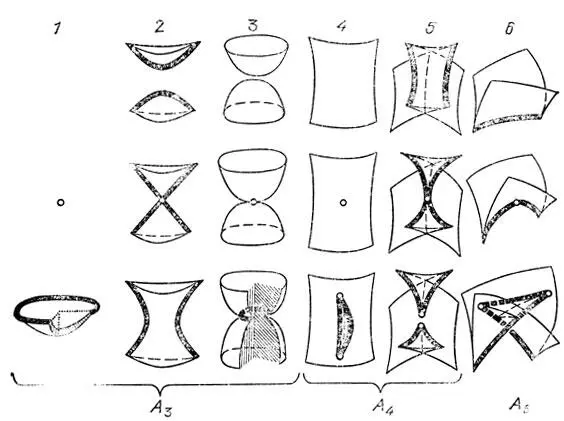
Рис. 44. Типичные переустройки каустик в трехмерном пространстве: серия А

Одна из этих метаморфоз (1) описывает рождение новой каустики "из воздуха". Мы видим, что вновь родившаяся каустика имеет вид блюдца с заостренными краями. Через время t после рождения длина и ширина блюдца порядка √t, глубина порядка t, а толщина порядка t √t.

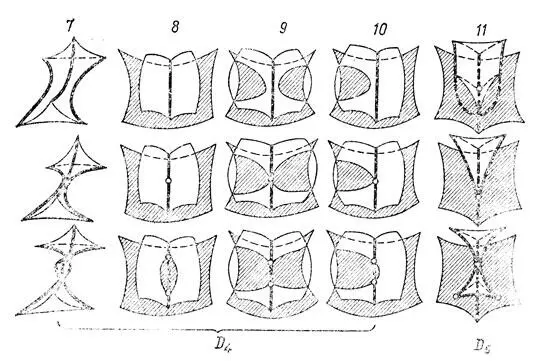
Рис. 45. Типичные перестройки каустик в трехмерном пространстве: серия D

Каустика может сделаться видимой, если на пути светового пучка имеется рассеивающая среда (пыль, туман). В. М, Закалюкин предположил, что каустики этого вида наблюдатели описывают как летающие блюдца.

Ребра возврата движущихся в трехмерном пространстве каустик заметают поверхность бикаустики . Особенности бикаустик общего положения, соответствующих различным метаморфозам рис. 44 и 45, изображены на рис. 46.

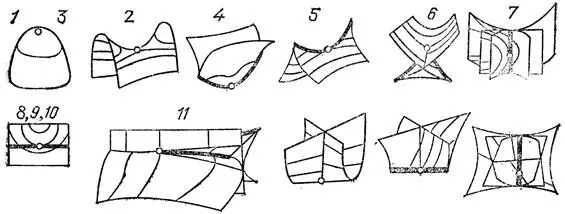
Рис. 46. Типичные особенности бикаустик

Как известно, лучи описывают распространение волн (скажем, световых) лишь в первом приближении; при более точном волновом описании появляется новый существенный параметр — длина волны (лучевое описание пригодно лишь в случае, когда эта длина мала по сравнению с характерным геометрическим размером системы).

Интенсивность света вблизи каустики больше, а вблизи ее особенностей еще больше. Коэффициент усиления оказывается пропорциональным l -α, где l — длина волны, а показатель α — рациональное число, зависящее от характера особенности. Для простейших особенностей значения α таковы:

Каустика 1/6

Ребро возврата 1/4

Ласточкин хвост 3/10

Пирамида 1/3

Кошелек 1/3

Таким образом, ярче всего светятся точечные особенности тина пирамиды и кошелька. В случае движущейся каустики в отдельные моменты времени могут возникать более яркие особенности [4] Все перечисленные особенности классифицируются по типам A k , D k , о которых подробнее рассказано выше. А 5, D 5(см. рис. 44, 45, α = 1/3 для А 5, 3/8 для D 5).

Если свет настолько интенсивен, что способен разрушать среду, то разрушение начнется в точках наибольшей яркости, поэтому показатель α определяет зависимость интенсивности разрушающего среду света от частоты.

Аналогичная описанной выше классификация особенностей каустик и волновых фронтов проведена в многомерных пространствах до размерности 10 (В. М, Закалюкин)

Предсказания теорией особенностей геометрии каустик, фронтов и их перестроек получили полное подтверждение в экспериментах, и сейчас даже кажется странным, почему эта теория не была построена лет двести назад. Дело, однако, в том, что соответствующий математический аппарат не тривиален [5] Первоначальное доказательство теоремы Уитни, о которой мы начали, занимало около 40 страниц; хотя окончательные геометрические результаты теории особенностей легко могут быть понятны и использованы, доказательства продолжают оставаться сложными. и связан с такими разделами математики, как классификации простых алгебр Ли и кристаллографических групп Кокстера, с теорией кос, теорией ветвления интегралов, зависящих от параметров, и т. д — он даже связан (довольно таинственным образом) с классификацией правильных многогранников в трехмерном евклидовом пространстве.