Владимир Арнольд - Теория катастроф

Рис. 32. Эволюция волнового фронта

Даже если начальный волновой фронт не имел особенностей, через некоторое время особенности начнут возникать. Например, при распространении возмущения внутрь эллипса, возникают особенности, изображенные на рис. 33. Эти особенности устойчивы (неустранимы малым шевелением начального фронта). Для гладкого начального фронта общего положения с течением времени будут образовываться лишь стандартные особенности такого же типа.

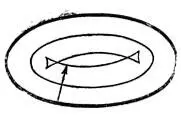
Рис. 33. Особенности эквидистант эллипса

Все иные особенности (например, особенность в центре сжимающейся окружности) при малом шевелении начального фронта рассыпаются на несколько особенностей стандартного вида.

В трехмерном пространстве на гладком волновом фронте общего положения с течением времени возникают лишь ребра возврата и стандартные особенности типа " ласточкин хвост ", изображенные на рис. 34 (попытайтесь разобраться в особенностях фронта, распространяющегося внутрь трехосного эллипсоида).

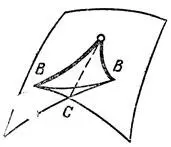
Рис. 34. Ласточкин хвост

Все более сложные особенности при малом шевелении фронта рассыпаются на соединенные ребрами возврата и линиями самопересечения ласточкины хвосты.

Ласточкин хвост можно определить как множество всех точек (а, b, с), таких, что многочлен х 3+ ах 2+ bх + с имеет кратный корень. У этой поверхности есть ребро возврата (В на рис. 34) и линия самопересечения (С на рис. 34).

Ласточкин хвост можно получить из пространственной кривой А = t 2, В = t 3, С = t 4: он образован всеми ее касательными.

Рассмотрим пересечения ласточкиного хвоста параллельными плоскостями общего положения (см. рис. 35).

Эти пересечения являются плоскими кривыми, При поступательном движении плоскости указанные кривые перестраиваются в момент, когда плоскость проходит через вершину хвоста. Перестройка (метаморфоза), происходящая при этом, в точности такая же, как метаморфоза волнового фронта на плоскости (например, при распространении возмущения внутрь эллипса).

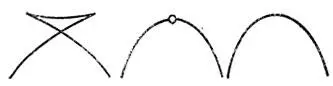
Рис. 35. Типичная перестройка волнового фронта на плоскости

Мы можем описать метаморфозы волновых фронтов на плоскости следующим образом. Рассмотрим наряду с основным пространством (в данном случае плоскостью) еще пространство-время (в данном случае трехмерное). Распространяющийся на плоскости волновой фронт заметает в пространстве-времени некоторую поверхность. Оказывается, саму эту поверхность всегда можно рассматривать как волновой фронт в пространстве-времени (" большой фронт "). В случае общего положения особенностями большого фронта будут ласточкины хвосты, ребра возврата и самопересечения, расположенные в пространстве-времени общим образом относительно изохрон (образованных "одновременными" точками пространства-времени). Теперь уже нетрудно сообразить, какие метаморфозы могут испытывать мгновенные волновые фронты на плоскости в случае общего положения; это перестройки сечений большого фронта изохронами.

Изучение метаморфоз волнового фронта при его распространении в трехмерном пространстве сводится таким же образом к исследованию сечений большого (трехмерного) волнового фронта в четырехмерном пространстве-времени трехмерными изохронами, Возникающие метаморфозы изображены на рис. 36.

Рис. 36. Типичные перестройки волновых фронтов в трехмерном пространстве

Изучение метаморфоз волновых фронтов было одной из задач, из которых возникла теория катастроф, однако даже в случае трехмерного пространства катастрофисты не сумели с ней справиться; рис. 36 появился лишь в 1974 г., когда в теории особенностей были разработаны новые методы (основанные на теории кристаллографических групп симметрий).

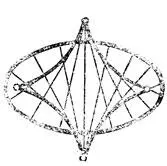
Рис. 37. Каустика эллипса

Наряду с волновыми фронтами процесс распространения возмущений описывается при помощи систем лучей . Например, распространение возмущений внутрь эллипса можно описать при помощи семейства внутренних нормалей к эллипсу (рис. 37). Это семейство имеет огибающую. Огибающая семейства лучей называется каустикой (т. е. "жгущей", так как в этих местах свет концентрируется), Каустика хорошо видна на внутренней поверхности чашки, освещенной солнцем. Радуга на небе также объясняется каустикой системы лучей, прошедших с полным внутренним отражением через каплю воды (рис. 38).

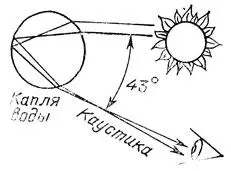
Рис. 38. Теория радуги Декарта

Каустика эллиптического фронта имеет четыре точки возврата. Эти особенности устойчивы: близкий к эллипсу фронт определит каустику с такими же особенностями. Все более сложные особенности каустик при малом шевелении рассыпаются на стандартные особенности: точки возврата (локальное уравнение — х 2= у 3) и точки самопересечения.

Система нормалей к поверхности в трехмерном пространстве также имеет каустику. Эту каустику можно построить, отложив на каждой нормали к поверхности радиус кривизны (поверхность, вообще говоря, имеет в каждой точке два различных радиуса кривизны, так что на нормали получается две точки каустики).

Нелегко представить себе, как выглядят каустики даже простейших поверхностей, например трехосного эллипсоида.

Каустики общего положения в трехмерном пространстве имеют лишь стандартные особенности. Эти особенности называются " ласточкин хвост ", " пирамида " и " кошелек " (см. рис. 39). Пирамида имеет три ребра возврата, касающиеся в вершине. Кошелек имеет одно ребро возврата и состоит из двух симметричных носов лодки, пересекающихся по двум линиям. Эти особенности устойчивы.

Рис. 39. Типичные особенности каустик в трехмерном пространстве

Все более сложные особенности каустик в трехмерном пространстве при малом шевелении рассыпаются на эти стандартные элементы .

Рассмотрим для одного и того же начального фронта (например, эллипса на плоскости) его каустику и фронты распространяющегося возмущения. Нетрудно понять, что особенности распространяющегося фронта скользят по каустике и заполняют ее .