Владимир Арнольд - Теория катастроф

Появились сотни научных и околонаучных публикаций, в которых теория катастроф применяется к столь разнообразным объектам, как, например, исследования биения сердца, геометрическая и физическая оптика, эмбриология, лингвистика, экспериментальная психология, экономика, гидродинамика, геология и теория элементарных частиц. Среди опубликованных работ по теории катастроф есть исследования устойчивости кораблей, моделирования деятельности мозга и психических расстройств, восстаний заключенных в тюрьмах, поведения биржевых игроков, влияния алкоголя на водителей транспортных средств, политики цензуры по отношению к эротической литературе.

В начале семидесятых годов теория катастроф быстро сделалась модной, широко рекламируемой теорией, напоминающей универсальностью своих претензий псевдонаучные теории прошлого века.

Математические статьи основоположника теории катастроф Р. Тома были переизданы массовым тиражом в карманной серии — событие, которого не было в математическом мире со времени возникновения кибернетики, у которой теория катастроф заимствовала многие приемы саморекламы.

Вслед за панегириками теории катастроф появились и более трезвые критические работы; некоторые из них также печатались в рассчитанных на широкого читателя изданиях под красноречивыми названиями вроде "А король-то — голый". Сейчас имеется уже много статей, специально посвященных критике теории катастроф. (См., например, обзор Дж. Гуккенхеймера "Споры о катастрофах" и пародию на критику теории катастроф.)

Источниками теории катастроф являются теория особенностей гладких отображений Уитни и теория бифуркаций динамических систем Пуанкаре и Андронова.

Теория особенностей — это грандиозное обобщение исследования функций на максимум и минимум. В теории Уитни функции заменены отображениями, т. е. наборами нескольких функций нескольких переменных.

Слово " бифуркация " означает раздвоение и употребляется в широком смысле для обозначения всевозможных качественных перестроек или метаморфоз различных объектов при изменении параметров, от которых они зависят.

Катастрофами называются скачкообразные изменения, возникающие в виде внезапного ответа системы на плавное изменение внешних условий. Чтобы понять, что такое теория катастроф, нужно вначале познакомиться с элементами теории особенностей Уитни.

В 1955 г. американский математик Хасслер Уитни опубликовал работу "Об отображениях плоскости на плоскость", заложившую основу новой математической теории — теории особенностей гладких отображений.

Отображение поверхности на плоскость — это сопоставление каждой точке поверхности точки плоскости. Если точка поверхности задана координатами (х 1, х 2) на поверхности, а точка плоскости координатами (y 1, у 2) на плоскости, то отображение задается парой функций у 1= f 1(х 1, х 2), у 2= f 2(х 1, х 2). Отображение называется гладким, если эти функции гладкие (т. е. дифференцируемые достаточное число раз, например многочлены).

Отображения гладких поверхностей на плоскость окружают нас со всех сторон. Действительно, большинство окружающих нас тел ограничено гладкими поверхностями. Видимые контуры тел — это проекции ограничивающих тела поверхностей на сетчатку глаза. Приглядываясь к окружающим нас телам, например к лицам людей, мы можем изучить особенности видимых контуров.

Уитни заметил, что в случаях "общего положения" [1] То есть для всех случаев, кроме некоторых исключительных. встречаются особенности лишь двух видов. Все другие особенности разрушаются при малом шевелении тел или направлений проектирования, в то время как особенности этих двух видов устойчивы и сохраняются при малых деформациях отображения.

Примером особенности первого вида — она названа складкой Уитни — является особенность, возникающая при проектировании сферы на плоскость в точках экватора рис. 1). В подходящих координатах это отображение задается формулами у 1= x 2 1, у 2= х 2. Проектирования поверхностей гладких тел на сетчатку в общих точках имеют именно такую особенность, и тут нет ничего удивительного. Удивительно то, что кроме этой особенности (складки) мы всюду встречаем еще ровно одну особенность, но практически никогда ее не замечаем.

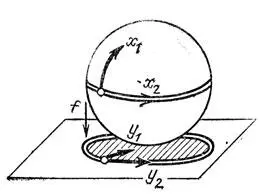
Рис. 1. Складка проектирования сферы на плоскость

Эта вторая особенность названа сборкой Уитни, и получается она при проектировании на плоскость поверхности, изображенной на рис. 2. Эта поверхность задана формулой у 1= х 3 1+ х 1х 2в пространстве с координатами (х 1, х 2, у 1) и проектируется на горизонтальную плоскость (х 2, у 1).

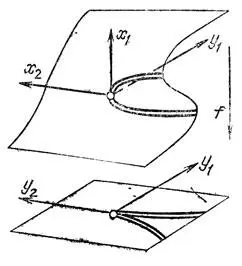
Рис. 2. Сборка проектирования поверхности на плоскость

Таким образом, отображение задается в локальных координатах формулами у 1= х 3 1+ х 1х 2, у 2= х 2.

На горизонтальной плоскости-проекции выделяется полукубическая парабола с точкой возврата (острием) в начале координат. Эта кривая делит горизонтальную плоскость на две части: меньшую и большую. Точки меньшей части имеют по три прообраза (в них проектируется три точки поверхности), точки большей части — лишь по одному, точки кривой — по два. При подходе к кривой из меньшей части два прообраза (из трех) сливаются и исчезают (в этом месте особенность — складка), при подходе к острию сливаются все три прообраза.

Уитни доказал, что сборка устойчива , т. е. всякое близкое отображение имеет в подходящей близкой точке подобную же особенность (т. е. такую особенность, что продеформированное отображение в подходящих координатах в окрестности указанной точки записывается теми же формулами, какими записывалось исходное отображение в окрестности исходной точки). Уитни также доказал, что всякая особенность гладкого отображения поверхности на плоскость после подходящего малого шевеления рассыпается на складки и сборки .

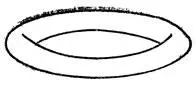
Рис. 3. Видимый контур тора

Таким образом, видимые контуры гладких тел общего положения имеют точки возврата в местах, где проектирования имеют сборки и не имеют других особенностей: приглядевшись, мы можем найти эти точки возврата в чертах каждого лица или тела. Рассмотрим, например, поверхность гладкого тора (скажем, надутой шины). Тор обычно рисуют так, как это изображено на рис. 3. Если бы тор был прозрачным, мы увидели бы видимый контур, изображенный на рис. 4: соответствующее отображение тора на плоскость имеет четыре сборки. Таким образом, концы линии видимого контура на рис. 3 — это точки возврата, в этих точках линия видимого контура имеет полукубическую особенность.

Читать дальше