Иэн Стюарт - Значимые фигуры. Жизнь и открытия великих математиков

Одну из первых попыток разрешить этот вопрос предпринял в XI в. Омар Хайям. Я упоминал его работу, связанную с кубическими уравнениями, но это был ни в коем случае не единственный его взнос в математическую копилку. Его «Комментарии к трудностям во введениях книги Евклида» построены на более ранней попытке Хасана ибн аль-Хайсама (в латинизированном варианте Альхазен) доказать аксиому о параллельных. Хайям логически отверг доказательство Ибн аль-Хайсама, как и другие «доказательства», и заменил их рассуждениями, в которых свел аксиому о параллельных к более интуитивно понятному утверждению.

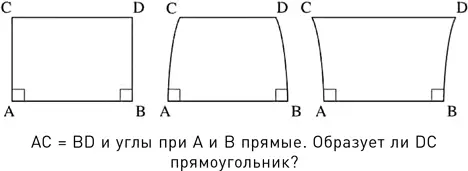
Один из ключевых чертежей Хайяма точно отражает суть проблемы. Его можно рассматривать как попытку построения прямоугольника – совершенно честную, можно сказать, попытку. Проводим прямую линию и строим под прямым углом к ней два отрезка прямых равной длины. Наконец, соединяем вторые концы этих отрезков, чтобы получить четвертую сторону прямоугольника. Готово!

Или нет? Откуда мы можем знать, что получившаяся в результате фигура – прямоугольник? В прямоугольнике все углы прямые, а противоположные стороны равны. На рисунке Хайяма мы видим, что два угла заведомо прямые и одна пара сторон одинакова. А что с остальными?

Да, согласен, все выглядит так, будто мы нарисовали прямоугольник, но это потому, что мы невольно пользуемся геометрией Евклида как мысленным ориентиром. И действительно, в Евклидовой геометрии мы можем доказать, что CD = AB и углы C и D тоже прямые. Однако этот вывод требует применения… той самой аксиомы о параллельных. Это едва ли можно считать удивительным, поскольку мы ожидаем, что CD будет параллельно AB. Если вы хотите доказать аксиому о параллельных на основании прочих аксиом Евклида, вам придется доказать, что Хайям нарисовал прямоугольник, не прибегая к аксиоме о параллельных. Более того, как понял Хайям, если вам удастся это доказать, дело будет сделано. Сама аксиома о параллельных напрямую из этого следует. Пытаясь избежать ловушки, связанной с попыткой доказать аксиому о параллельных, Хайям заменил ее на более простое предположение: «Две сходящиеся прямые пересекаются; невозможно, чтобы две сходящиеся прямые расходились в том же направлении, в каком они сходятся». И он вполне отчетливо понимал, что это действительно допущение.

Джованни Саккери развил чертежи Хайяма – а может быть, пришел к тем же результатам независимо, – но сделал при этом шаг назад, попытавшись с их помощью доказать аксиому о параллельных. Его «Евклид, очищенный от всех пятен» вышел в 1733 г. Он разбил свое доказательство на три возможных варианта, в зависимости от того, является ли угол C на рисунке прямым, острым (то есть меньшим, чем прямой) или тупым (большим, чем прямой). Саккери доказал, что, каким бы ни был тип угла C на одном таком чертеже, ровно таким же он будет и на любом другом чертеже подобного рода. Углы, о которых идет речь, все будут либо прямыми, либо острыми, либо тупыми. Таким образом, существует всего три общих случая, а не три случая для каждого прямоугольника в отдельности. Это большой шаг вперед.

Стратегия доказательства Саккери состояла в том, чтобы рассмотреть альтернативные варианты острых и тупых углов с целью отвергнуть их, распознав какое-либо противоречие. Сначала он предложил считать угол тупым. Это привело к результатам, которые он счел несовместимыми с другими аксиомами Евклида, – и отбросил этот вариант. Чтобы избавиться от варианта с острым углом, ему потребовалось намного больше времени, но в конечном итоге он вывел теоремы, противоречившие, по его мнению, остальным аксиомам. На самом деле это не так: если они чему-то и противоречат, то Евклидовой геометрии, аксиоме о параллельных и прочему. Так что Саккери думал, что доказал аксиому о параллельных, а мы сегодня считаем его работу большим шагом к логически непротиворечивым неевклидовым геометриям.

Отец Лобачевского, Иван, был мелким чиновником в учреждении, занимавшемся геодезической съемкой. Его мать Прасковья, как и отец, была родом из Польши. Отец Николая умер, когда мальчику было семь лет, и мать с детьми переехала в Казань. После окончания школы Николай в 1807 г. поступил в Казанский университет. Начал он с изучения медицины, но вскоре переключился на математику и физику. Среди его профессоров был друг Гаусса и бывший школьный учитель Бартельс.

В 1811 г. Лобачевский получил степень магистра математики и физики; он стал преподавателем, затем экстраординарным профессором, а к 1822 г. и полным профессором. Университетом в тот момент руководили консерваторы и ретрограды, опасавшиеся всего нового, особенно в естественных науках и философии. Они считали то и другое своего рода опасными следствиями Французской революции и угрозой православию – господствующей религии в России того времени. В результате академическая жизнь застопорилась, лучшие преподаватели (среди них и Бартельс) уехали, многих уволили; научные стандарты заметно снизились. Это было не лучшее место для человека, которому предстояло разрушить косную традицию в геометрии, насчитывавшую не одну тысячу лет; к тому же откровенность и независимость отнюдь не облегчали Лобачевскому жизнь. Тем не менее он продолжал математические исследования, и читаемые им курсы были образцом ясности и логичности изложения.

Административная карьера Лобачевского началась со вступления в университетскую комиссию по содержанию зданий и развивалась вполне успешно. Он приобретал новое оборудование для физической лаборатории и книги для библиотеки; руководил обсерваторией, был деканом физико-математического факультета с 1820 по 1825 г., заведовал библиотекой с 1825 по 1835 г. Его разногласия с властями сгладились, когда на престол взошел Николай I, который спокойнее относился к политике и управлению. Царь снял попечителя (формального главу) университета Михаила Магницкого с должности. Пришедший ему на смену Михаил Мусин-Пушкин стал надежным союзником Лобачевского, и в 1827 г. тот был назначен ректором университета. Назначение оказалось очень успешным; Лобачевский проработал на этом посту 13 лет, и за это время университет обзавелся новыми зданиями – библиотекой, а также корпусом для занятий астрономией, медициной и физикой. Он поощрял исследования в области изящных искусств и физики, увеличивал число студентов. Благодаря его быстрым и решительным действиям удалось минимизировать ущерб от эпидемии холеры в 1830 г. и пожара в 1842 г.; царь прислал Лобачевскому благодарственное письмо. Все это время он не переставал читать лекции по математическому анализу и физике, а также публичные лекции на разные темы.