Иэн Стюарт - Значимые фигуры. Жизнь и открытия великих математиков

В 1868 г. Эудженио Бельтрами предложил конкретную модель гиперболической геометрии: внутренняя геометрия поверхности, известной как псевдосфера и имеющей постоянную отрицательную кривизну. Он интерпретировал этот результат как наглядное подтверждение того, что на самом деле гиперболическая геометрия не есть нечто новое; это просто Евклидова геометрия, приспособленная к соответствующей поверхности. При этом он упустил из виду более глубокий логический вывод: эта модель доказывает непротиворечивость гиперболической геометрии, так что аксиома о параллельных не может быть выведена из других аксиом Евклида. Оуэль понял это в 1870 г., когда перевел статью Бельтрами на французский.

Подобрать модель для эллиптической геометрии было проще. По существу, это геометрия больших окружностей на сфере, с одной оговоркой. Большие окружности пересекаются в двух диаметрально противоположных точках, а не в одной точке, и потому не удовлетворяют остальным аксиомам Евклида. Чтобы исправить ситуацию, достаточно переопределить «точку» как «пару диаметрально противоположных точек» и рассматривать большую окружность как пару диаметрально противоположных полуокружностей. Это пространство – формально сфера с попарно отождествленными противоположными точками – обладает постоянной положительной кривизной, унаследованной от сферы.

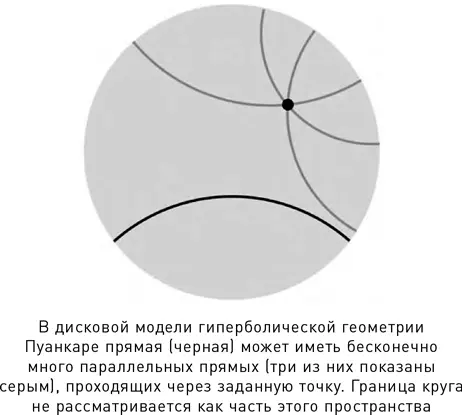
Тем временем неевклидова геометрия начала потихоньку появляться и в других областях математики, в первую очередь в комплексном анализе, где она связана с преобразованием Мёбиуса, отображающим окружности (и прямые) на окружности (и прямые). Вейерштрасс прочел лекцию на эту тему в 1870 г. Клейн, двигавшийся в том же направлении, уловил суть и обсудил эту идею с Софусом Ли. В 1872 г. он составил важный документ – Эрлангенскую программу, в которой определил геометрию как науку об инвариантах групп преобразований. Такой подход объединил почти все варианты, на которые успела разделиться к тому времени геометрия; основным исключением из этого перечня стала Риманова геометрия для поверхностей непостоянной кривизны, где подходящих групп преобразований просто нет. Пуанкаре зашел еще дальше, предложив, в частности, собственную модель гиперболической геометрии. Пространство в ней представляет собой внутренность круга, а «прямые» линии – дуги окружностей, подходящих к границе круга под прямыми углами.

Позже гиперболическая геометрия стала одним из стимулов к появлению Римановой теории искривленных пространств любой размерности (многообразий), на которой построена теория гравитации Эйнштейна (глава 15). В число ее приложений в современной математике входят комплексный анализ, специальная теория относительности, комбинаторная теория групп и гипотеза (теперь уже теорема) о геометризации Тёрстона в топологии трехмерных многообразий (глава 25).

4 июня 1832 г. французская газета Le Precursor сообщила о сенсационном, хотя и ни в коем случае не уникальном в своем роде, событии:

Париж, 1 июня. Вчера прискорбная дуэль лишила точные науки молодого человека, который подавал величайшие надежды; в последнее время, однако, его прославленная ранняя зрелость отошла в тень под влиянием его политической деятельности. Молодой Эварист Галуа… дрался с одним из своих старых друзей… не менее известным в политических кругах. Говорят, что причиной схватки стала любовь. В качестве оружия был выбран пистолет, но, поскольку из-за старой дружбы противники были не в состоянии смотреть друг на друга, решать судьбу свою они доверили слепой судьбе. Стреляли они практически в упор; у каждого был пистолет, но лишь один пистолет был заряжен. Галуа был прошит пулей своего противника насквозь; его отвезли в больницу Кошен, где он и умер примерно через два часа. Ему было 22 года. Его противник L. D. чуть моложе.

Ночь перед дуэлью Галуа посвятил краткому изложению на бумаге своих математических исследований, основная часть которых была сосредоточена на использовании особых наборов перестановок, которые он называл «группами», для определения того, может ли некоторое алгебраическое уравнение быть решено в формульном виде. Он описал также связь этой идеи с особыми функциями, известными как эллиптические интегралы. Из результатов его работы прямо следует, что не существует алгебраической формулы для решения обобщенного уравнения пятой степени – вопрос, ставивший математиков в тупик не одно столетие, прежде чем Паоло Руффини опубликовал почти полное, но ужасно длинное доказательство, а Нильс Хенрик Абель получил доказательство попроще.

До сего дня существует несколько мифов об Эваристе Галуа, несмотря на все попытки историков разобраться в его биографии и установить истинный ход событий. Документальные свидетельства обрывочны и иногда противоречивы. К примеру, кто был его противником на дуэли? На газетную статью полагаться не стоит – начать с того, что журналисты даже возраст погибшего называют неправильно, – и многое остается неясным. А вот значимость математики Галуа никаких сомнений не вызывает. Понятие группы перестановок стало одним из первых существенных шагов к теории групп, а она, в свою очередь, оказалась ключом к глубокой математике симметрии; даже в наше время в этой области ведутся серьезные исследования. Группы сегодня играют центральную роль во многих областях математики, не обойтись без них и в математической физике. Они имеют важные приложения в области формирования структур во многих областях физической и биологической науки.

Отец Эвариста Николя-Габриэль, убежденный республиканец, стал мэром Бур-ля-Рена в 1814 г., после того как Людовик XVIII вновь стал королем. Его мать Аделаида-Мари (урожденная Демант) была хорошо образованной дочерью юридического консультанта. Она изучала религию и классические языки и до 12 лет сама обучала Эвариста дома. Мальчику легко давалась латынь, он заскучал – и нашел утешение в математике. Эварист читал продвинутые работы: «Начала геометрии» Лежандра и оригинальные труды Абеля и Лагранжа о решении полиномиальных уравнений «в радикалах». Этот термин относится к алгебраическим формулам, выражающим решения уравнений через коэффициенты с использованием базовых арифметических операций и извлечения корней второй, третьей и более высоких степеней. Вавилоняне в свое время решали в радикалах квадратные уравнения, а алгебраисты Возрождения делали то же самое с уравнениями третьей и четвертой степеней. Теперь же становилось очевидно, что эти методы выдохлись. Абель в 1824 г. доказал, что обобщенное уравнение пятой степени не может быть решено в радикалах, а в 1826 г. опубликовал развернутое доказательство.