Иэн Стюарт - Значимые фигуры. Жизнь и открытия великих математиков

Харди однажды написал, что каждое положительное целое число было личным другом Рамануджана, и проиллюстрировал это анекдотом о посещении Рамануджана в больнице. «Я приехал к нему в такси номер 1729 и заметил в разговоре, что это число показалось мне каким-то скучным и что, как я надеялся, это не дурная примета. “Нет, – ответил Рамунаджан, – это очень интересное число; это самое маленькое число, которое можно выразить как сумму двух кубов двумя разными способами”».

Если точнее,

1729 = 1 3+ 12 3= 9 3+ 10 3,

и это действительно самое маленькое число, обладающее таким свойством.

История колоритная, но я не могу отделаться от ощущения, что со стороны Харди это был подготовленный экспромт; Харди просто пытался подбодрить больного друга, поманив его интересной задачей. Конечно, большинство людей не заметили бы эту особенность числа 1729, но Рамануджан, несомненно, должен был сразу распознать ее. И правда, многие математики, особенно те из них, кто интересуется теорией чисел – и Харди среди них, – должны были знать об этом. Почти невозможно себе представить, чтобы математик, посмотрев на число 1729, не подумал о числе 1728, которое представляет собой 12 в кубе. Трудно также не заметить, что 1000 – это 10 в кубе, а 729 – 9 в кубе.

Как бы то ни было, рассказ Харди привел к появлению в теории чисел не слишком крупной, но интересной концепции: числа такси; n -е число такси есть наименьшее число, которое можно выразить как сумму двух положительных кубов n различными способами. Вот следующие два числа такси:

87 539 319,

6 963 472 309 248.

Чисел такси существует бесконечно много, но известны лишь первые шесть из них.

К 1917 г. Рамануджан вернулся в свои комнаты, одержимый математикой до такой степени, что ничто другое для него уже не имело значения. Он часто работал день и ночь, а затем падал в изнеможении и спал часов 20 подряд. Это не приносило пользы его здоровью, а война вызывала дефицит фруктов и овощей, которыми он питался. К весне Рамануджана поразила какая-то нераспознанная, но, вероятно, неизлечимая болезнь. Его положили в маленькую частную больницу для пациентов из Тринити-колледжа. На протяжении двух следующих лет он консультировался у восьми, если не больше, врачей и побывал по крайней мере в пяти больницах и санаториях. Врачи подозревали язву желудка, затем рак, затем заражение крови; но в конечном итоге решили, что это, скорее всего, туберкулез, и лечили Рамануджана в основном именно от этой болезни.

Рамануджану наконец-то – слишком поздно – досталось академическое признание. Он стал первым индийцем, которого избрали членом Королевского общества, и Тринити-колледж тоже избрал его своим членом. Это придало Рамануджану новые силы, и он вновь взялся за математику. Но здоровье не улучшалось, и были подозрения, что виной тому – климат Англии. В апреле 1919 г. Рамануджан вернулся в Индию. Долгое путешествие не прошло для него даром, и к моменту прибытия в Мадрас здоровье его вновь ухудшилось. В 1920 г. Рамануджан умер в Мадрасе, оставив вдову. Детей у них не было.

С математикой Рамануджана можно познакомиться по четырем основным источникам: это опубликованные статьи, три переплетенных блокнота, квартальные отчеты Мадрасскому университету и неопубликованные рукописи. Четвертый «утерянный» блокнот – связка разрозненных листков – вновь обнаружил в 1976 г. Джордж Эндрюс, но некоторые рукописи до сих пор не найдены. «Записные книжки Рамануджана» в трех томах, включающие доказательства всех его формул, вышли под редакцией Брюса Берндта.

У Рамануджана была необычная биография и не было формального математического образования. Вряд ли стоит удивляться тому, что его математика весьма специфична. Самой сильной стороной его таланта была немодная область математики – производство остроумных и замысловатых формул. Рамануджан был преимущественно человеком формулы, и в этом ему не было равных, за исключением нескольких старых мастеров, таких как Эйлер или Якоби. «В каждой из формул Рамануджана всегда кроется больше, чем видно на первый взгляд», – писал Харди. Большая часть его результатов имеет отношение к бесконечным рядам, интегралам и цепным дробям. В качестве примера цепной дроби можно привести выражение

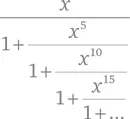
которое было написано на последней странице его письма в составе по-настоящему жуткой, но правильной формулы. Некоторые из своих формул Рамануджан применял в теории чисел, где его особо интересовала аналитическая теория чисел, которая ищет простые приближения для таких величин, как число простых чисел до заданного предела – теорема о простых Гаусса (глава 10) – или среднее число делителей у заданного числа.

Его публикации во время пребывания в Кембридже готовились под влиянием общения с Харди и были написаны в традиционном стиле, со строгими доказательствами. Результаты, записанные в его блокнотах, выглядят совершенно иначе. Поскольку он был самоучкой, представления о доказательстве у него были совсем не строгие. Для Рамануджана было достаточно, если при помощи численных данных пополам с формальными рассуждениями он мог получить правдоподобный вывод – и при этом интуиция говорила ему, что ответ верен. Как правило, его результаты были верны, но в доказательствах часто имелись пробелы. Иногда эти пробелы мог заполнить любой компетентный математик, а иногда для этого требовались нестандартные аргументы. В редких случаях в его результатах обнаруживалась ошибка. Берндт утверждает, что, если бы Рамануджан «мыслил как хорошо подготовленный математик, он не стал бы записывать многие из тех формул, которые он, по собственному мнению, доказал» и математика от этого серьезно пострадала бы.

Хорошим примером может служить результат, который Рамануджан называл своей «мастер-формулой» [28] Мастер-формула Рамануджана гласит, что если есть комплекснозначная функция, то где Г( s ) есть Эйлерова гамма-функция. – Прим. авт. . Его доказательство включает в себя разложения в ряд, смену порядка суммирования и интегрирования и другие аналогичные приемы. Поскольку он использует при этом бесконечные процессы, каждый его шаг сопряжен с опасностью. Величайшие аналитики почти весь XIX век разбирались, когда подобные процедуры допустимы. Условия, которые, по Рамануджану, делают его формулу верной, чрезвычайно недостаточны. Тем не менее почти все результаты, которые он выводит из своей мастер-формулы, верны.

Часть самых поразительных работ Рамануджана относится к теории разбиений – одного из разделов теории чисел. Взяв некоторое натуральное число, мы спрашиваем, сколькими способами его можно разбить на слагаемые, то есть записать в виде суммы меньших натуральных чисел. К примеру, число 5 можно разбить на слагаемые семью разными способами: