Альфред Реньи - Диалоги о математике

Синьора Никколини . Понимаю. Но, по теории Коперника, Земля не движется по прямой, ведь она движется вокруг Солнца. Не похоже ли это на тот случай, когда корабль изменяет направление движения, которое, как вы сказали, может быть замечено даже в закрытой каюте?

Галилей . Если корабль меняет направление движения медленно, заметить это очень трудно — мы чувствуем только резкие изменения. Земля делает поворот вокруг Солнца за один год, а в течение нескольких часов направление движения меняется очень мало. Это сильно затрудняет наблюдения.

Синьора Никколини . А что вы скажете о вращении Земли вокруг собственной оси? Как я поняла, согласно Копернику, Земля делает полный оборот за сутки. Можем ли мы как-нибудь заметить это движение?

Галилей . Теперь я вижу, вы хорошо понимаете, какое именно решающее доказательство я ищу. Однако пока я его не нашел. Но, уверен, наука скоро найдет его.

Синьора Никколини . У меня еще один вопрос. Я не совсем поняла, что вы сказали о законах природы, написанных на языке математики. Мне было бы понятнее, если бы вы привели какой-нибудь пример.

Галилей . Попрошу вас, подойдите к окну. Взгляните на этот мяч. Я бросаю его. Наблюдайте, как он будет падать на землю. Что вы заметили?

Синьора Никколини . Мне кажется, что он падает все быстрее и быстрее.

Галилей . Вы правы. Но как изменяется скорость? Если вы рассмотрите расстояния, которые проходит мяч в равные промежутки времени, то увидите, что они соотносятся как нечетные числа: за вторую секунду мяч проходит расстояние в три раза большее, чем за первую, за третью — в пять раз, за четвертую — в семь раз и т. д. Другими словами, скорость падающего тела увеличивается равномерно — это движение равномерно-неравномерное. Раньше схоласты имели дело с таким движением, но они не использовали математики, а это движение не может быть по-настоящему понято без нее.

Синьора Никколини . Очень интересно.

Галилей . Погодите, закончим наш разговор о падающих телах. Все, что я сказал ранее, может быть выражено следующими словами: скорость тела возрастает пропорционально времени. Теперь рассмотрим расстояние, которое проходит падающее тело с начала падения до какого-то произвольного момента. Обозначим расстояние, которое проходит тело в первую секунду, через а. Тогда, как я уже сказал, расстояние, пройденное во вторую секунду, будет равно За, а сумма расстояний за две первые секунды За+а=4а. Вы помните, что я говорил о расстоянии за третью секунду?

Синьора Никколини . Конечно, оно равно 5а, поэтому за три секунды расстояние станет равным 4а+5а=9а, за четвертую секунду проходится путь в 7а, следовательно, полный путь, пройденный т. елом за четыре секунды, равен 16а.

Галилей . Таким образом, падающее тело за две секунды проходит путь, равный 4а, за три секунды 9а, за четыре секунды 16а. Замечаете вы какую-нибудь закономерность?

Синьора Никколини . Мне кажется, расстояние, проходимое телом с начала падения, пропорционально квадрату времени. Не так ли?

Галилей . Да, это верно, и не только когда время равно 1, 2, 3, 4… секунд, но и в общем случае.

Синьора Никколини . Как можно доказать этот закон для общего случая?

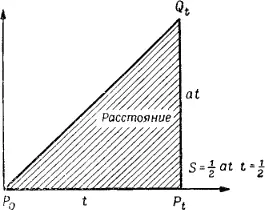
Галилей . Очень просто. Нарисуйте прямую линию. Выберите точку Р 0на этой линии, которая будет соответствовать моменту начала движения. Тогда точка P t на той же линии, лежащая справа от точки Р 0 , соответствует времени t с начала движения. В точке P t проведем перпендикуляр к линии P 0 P t и выберем на нем такую точку Q t , расстояние от которой до P t равно скорости падающего тела в момент t. Так как скорость пропорциональна времени, то точка Q t будет лежать на прямой, начинающейся в точке Р 0 .

Синьора Никколини . Но как можно на этой фигуре найти полное пройденное расстояние?

Галилей . Очень просто — расстояние, пройденное вплоть до момента t, равно площади треугольника I' 0 P tQ t.

Синьора Никколини . Почему?

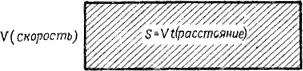
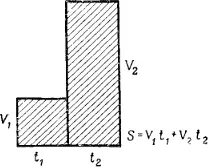
Галилей . При постоянной скорости расстояние равно произведению скорости на время. Пройденное расстояние равно площади прямоугольника, одна сторона которого изображает время, а вторая скорость. Если скорость изменяется, ситуация становится более сложной, но расстояние все так же равно площади. Например, если сначала скорость постоянна, а потом сразу увеличивается до какой-то величины, то путь равен площади фигуры, состоящей из двух прямоугольников. Если скорость изменяется несколько раз, но между двумя последовательными изменениями остается постоянной, то путь равен площади фигуры, состоящей из нескольких прямоугольников. Если скорость, начинающаяся с нуля, изменяется непрерывно и равномерно, то путь равен площади треугольника. Чтобы понять это, вы должны рассмотреть треугольник, как бы состоящий из бесконечного числа бесконечно тонких прямоугольников разной высоты.

Синьора Никколини . Удивительно. Этот вопрос рассматривается в вашей книге по математической теории движения?

Галилей . Да, и множество других. Подобно тому как можно вычислить, где будет падающий камень через две или три секунды после начала падения, можно показать, что траектория камня, брошенного в любом направлении, — парабола. Этот вопрос интересен не только в практическом смысле, но также и тем, что благодаря ему я могу показать, как следует комбинировать различные движения. И я никак не пойму, почему никто, кроме, возможно, Архимеда, тщательно не исследовал, что случается, когда роняют или бросают камень. Ведь еще Птолемей пытался подсчитать видимые орбиты Солнца, Луны и планет, наблюдения за которыми велись изо дня в день и из года в год. Более того, я утверждаю — даже если меня снова заподозрят в ереси, — что движение здесь, на Земле, подчиняется тем же законам, что и в небе .

Синьора Никколини . Итак, Вселенная похожа на большие часы, у которых можно точно подсчитать, как поворачиваются колеса — и самые маленькие, и самые большие.

Галилей . Эти удивительные закономерности составляют только одну главу книги природы! Но там также имеется много других закономерностей, непредсказуемых, случайных событий.