Йэн Стюарт - Укрощение бесконечности. История математики от первых чисел до теории хаоса [litres]

Мы определяем искусство предположений, или стохастическое искусство, как искусство точной оценки вероятностей, чтобы в наших суждениях и действиях мы всегда опирались на то, что признано лучшим, наиболее приемлемым, наиболее определенным или рекомендуемым; это единственная основа для мудрости философа и благоразумия государственного мужа.

Возможно, правильнее было бы назвать эту книгу «Искусство догадок».

Бернулли принимал как данность, что чем больше количество испытаний, тем лучше можно будет оценить вероятность.

Предположим, без вашего ведома в урну поместили 3000 белых камней и 2000 черных. Пытаясь определить количество этих камней, вы вынимаете один камень за другим (каждый раз возвращая его обратно) и обращаете внимание, как часто попадаются белый и черный камни. Насколько часто вам придется так делать: 10 раз, или 100 раз, или 1000 раз и т. д., что более вероятно, ‹…› чтобы [в итоге] выбранные белые и черные камни находились в том же соотношении 3:2, что и в урне?

Здесь Бернулли не только задал один из основных вопросов, но и изобрел стандартный иллюстративный пример – камни в урне. Он явно был уверен, что пропорция 3:2 будет разумным результатом, но понимал, что в реальности эксперименты могут лишь приблизиться к ней. Однако он был уверен еще и в том, что при достаточном количестве попыток эта аппроксимация будет всё точнее и точнее.

Тут была своя трудность, надолго затормозившая развитие этой науки. В подобных экспериментах всегда есть определенная возможность , что по чистой случайности все вынутые из урны камни окажутся белыми. Нет достаточно надежной гарантии, что пропорция будет всегда стремиться к 3/ 2. В лучшем случае мы можем утверждать, что с очень высокой вероятностью числа будут приближаться к этому значению. Но тогда возникает риск круговой логики: мы используем пропорции, полученные в опытах, чтобы оценить вероятности, но также используем вероятности, чтобы получить этот вывод. Как мы видим, что вероятность вытащить только белые камни крайне мала? Если мы добиваемся этого в большем числе испытаний, то должны учесть и возможность того, что результат по какой-то причине окажется ошибочным. Единственным выходом из этого тупика кажется проведение еще большего числа испытаний, чтобы показать, как низка вероятность такого результата. В итоге мы попадаем в состояние, слишком напоминающее бесконечное движение по кругу.

К счастью, первые исследователи теории вероятностей не позволили этому логическому препятствию себя остановить. Как и в случае с исчислением, они знали, чего хотят и как этого добиться. Философские суждения были для них менее важны, чем поиск ответов на вопросы.

Книга Бернулли содержала много важных идей и результатов. Один из них, закон больших чисел , показывает нам, в каком именно смысле долгосрочные наблюдения за пропорциями в испытаниях соответствуют вероятностям. Главным образом он доказывает следующее: вероятность того, что пропорция не будет близка к правильной вероятности, стремится к нулю при неограниченном росте количества испытаний.

В 1710 г. Джон Арбетнот представил в Королевское общество Великобритании статью, в которой с помощью теории вероятностей доказывал существование Бога. Он проанализировал ежегодное число крещений младенцев мужского и женского пола в 1629–1710 гг. и обнаружил, что мальчиков было немногим больше, чем девочек. Более того, эта разница оставалась практически неизменной каждый год. Этот факт был уже тогда хорошо известен, но Арбетнот вычислил вероятность того, что пропорция постоянна. Его результат получился очень маленьким: 2 −82. Он указал, что если такой эффект наблюдается во всех странах, во все времена и у всех народов, то шанс был бы еще меньше. Из чего он сделал вывод, что всё происходит не по случайности, а благодаря божественному провидению.

А в 1872 г. Фрэнсис Гальтон использовал теорию вероятностей для оценки действенности молитв исходя из того, что огромное число людей каждый день возносят молитвы о здоровье королевской семьи. Он собрал данные по «средней продолжительности жизни мужчин из различных сословий, проживших более 30 лет, от 1758 до 1843 г.», добавив, что «исключил смерти от несчастного случая». В его выборку вошли аристократы, королевская семья, духовенство, адвокаты, врачи, дворяне, купцы, офицеры армии и флота, деятели науки, литературы и искусства. Он обнаружил, что «властители буквально самые коротко живущие из всех состоятельных слоев общества. Таким образом, молитвы совершенно бесполезны, если только не прибегнуть к весьма спорной гипотезе, будто условия жизни королевской семьи настолько фатальны, что отчасти, хотя и не полностью, могут нейтрализовать эффект народных молитв».

Другая базовая теорема может быть рассмотрена для случая повторных бросков бракованной (смещенной) монеты с вероятностью p для выпадения орла и q = 1 – p для выпадения решки. Если монету бросить дважды, какова будет вероятность того, что орел выпадет 2, 1 или 0 раз? Ответ Бернулли был p 2, 2 pq и q 2. Таковы результаты при разложении выражения ( p + q ) 2в p 2+ 2 pq + q 2. А если монету бросить три раза, вероятность того, что орел выпадет 3, 2, 1 или 0 раз, равна последовательности множителей в выражении ( p + q ) 3= p 3+ 3 p 2 q + 3 q 2 p + q 3.

В более общем виде, если монету бросить n раз, вероятность выпадения орла m раз будет равна:

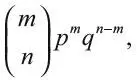
т. е. соответствующему члену в разложении ( p + q ) n.

В 1730–1738 гг. Абрахам де Муавр продолжил опыты Бернулли со смещенной монетой. Когда m и n достаточно велики, трудно точно вычислить биномиальный коэффициент, и де Муавр вывел приблизительную формулу, соответствующую биномиальному распределению Бернулли, которое сейчас мы называем функцией ошибок или нормальным распределением :

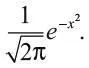
Де Муавр заслуженно считается первым математиком, явно показавшим эту связь. Это стало краеугольным камнем в развитии как теории вероятностей, так и статистики.

Основной проблемой теории вероятностей оставалось определение вероятности. Даже самые простые задачи – на которые все знают ответ – были чреваты логическими затруднениями. Если мы бросаем монету, то в длительном периоде ожидаем равного числа выпадений орлов и решек, и вероятность для каждого варианта равна 1/ 2.