Мартин Гарднер - Этот правый, левый мир

Предположим, однако, что существует трансцендентный мир, мир 4-пространства, не доступный нашим органам чувств, за пределами способностей нашего воображения. Как же будут выглядеть с точки зрения гиперличности в таком гиперпространстве два асимметричных телесных предмета, которые подобно многогранникам с рис. 41 являются зеркальным отражением друг друга? Математика дает ясный и недвусмысленный ответ: эти многогранники будут идентичны и полностью наложимы один на другой!

Чтобы понять это, посмотрим мысленно на 2-пространство и на две находящиеся в нем асимметричные фигуры, изображенные на рис. 42. Двумерцы, живущие на плоскости, были бы так же озадачены этими фигурами, как Канта озадачивали его уши и их отражение в зеркале. Как могут быть эти фигуры столь похожи, спросят себя двумерцы, и в то же время неналожимы? Мы, жители 3-пространства, можем это понять. Фигуры в самом деле одинаковы. Это только несчастные Двумерцы, сидящие в своем двумерном мире, глядят на все через очки евклидова 2-пространства и не могут себе представить, что эти фигуры наложимы. Мы можем это доказать, просто взяв одну из них и предварительно перевернув, наложить на другую. Если мы вернем перевернутую фигуру в плоскость, расположив ее рядом с первой, то для двумерцев они обе будут абсолютно одинаковы во всех отношениях, включая «знак асимметрии». Поскольку двумерцы не могут себе представить 3-пространство, они подумают, что произошло чудо. Твердый асимметричный объект перешел в свое зеркальное изображение! И в то же время мы с этим предметом ничего не сделали. Мы его не растянули, не повредили, вообще никак не изменили. Мы только изменили его ориентацию в 2-пространстве — его положение по отношению к другим предметам в пространстве.

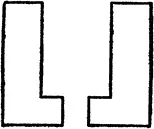
Два асимметричных многогранника с рис. 41 точно так же абсолютно одинаковы и могут быть наложены друг на друга. Только потому, что мы не можем взглянуть на них через трансцендентные очки 4-пространства, они кажутся нам разными. Если бы мы могли вращать их в гиперпространстве — перевернуть их, так сказать, через четвертое измерение, — то получили бы пару абсолютно одинаковых конгруэнтных многоугольников.

Кант, конечно, таких взглядов не выражал. Тем не менее я думаю, что если серьезно, используя всю имеющуюся информацию, попытаться воспринять окончательную точку зрения Канта на все сущее, то не будет никакого легкомыслия в предположении, что Кант вполне мог бы рассуждать таким образом, будь к его услугам математические знания XX столетия.

Лейбниц тоже, я убежден, интуитивно понимал еще не открытые тогда высшие евклидовы пространства. Он однажды рассматривал вопрос о том, что произошло бы, превратись весь мир и все вещи в нем в свои зеркальные изображения. Он пришел к заключению, что ничего бы не случилось. Не имело бы смысла говорить, что такое превращение вообще произошло, потому что нет способа заметить это изменение. Спрашивать, почему бог создал мир так, а не наоборот, значит, по словам Лейбница, задавать «совершенно никчемный вопрос».

Когда мы пытаемся ответить на этот вопрос с точки зрения высших евклидовых пространств, мы видим, что Лейбниц прав. Все, что требуется для того, чтобы «реверсировать» Флатландию на листке бумаги, это перевернуть листок и посмотреть на фигуры с другой стороны. Можно даже не переворачивать бумагу. Представьте себе Флатландию, расположенную на вертикальном листе стекла посреди комнаты. Когда вы смотрите на нее с одной стороны, это левый мир. Обойдите стекло кругом, и вы увидите правый мир.

Упражнение 11.Когда мистер Смит пытался открыть стеклянную дверь в банк, он с удивлением увидел на ней надпись большими черными буквами ДОХВ. Что значит это слово?

Флатландия совершенно не меняется, когда вы смотрите на нее с другой стороны. Происходит изменение только в расположении Флатландии в 3-пространстве относительно вас. Точно таким же образом житель 4-пространства может посмотреть на обыкновенный штопор с одной стороны и увидит правую спираль, а затем, зайдя с другой стороны, он увидит в том же самом штопоре левую спираль. Если бы он мог взять наш штопор, перевернуть и возвратить в наше пространство, нам показалось бы, что мы видим чудо. На наших глазах штопор исчез бы и появился в зеркальной форме.

Энантиоморфные предметы одинаковы не только по всем своим метрическим свойствам, они и топологически идентичны. Хотя правый узел на замкнутой петле нельзя переделать в левый, они топологически эквивалентны. Маленькие дети схватывают это быстрее, чем взрослые. Жан Пиаже и Бэрбел Инхелдер в своей книге «Детское представление о пространстве» приводят сильные доводы, подтвержденные экспериментально, в пользу того, что дети действительно выучиваются различать топологические свойства еще до того, как привыкают узнавать евклидовы свойства формы и разницу между правым и левым. Маленькие дети, например, когда их просят скопировать треугольник, очень часто рисуют круг. Углы и стороны треугольника для них менее заметны, чем свойство замкнутости кривой. Они не заметят разницы между цветным кружком, раскрашенным по часовой стрелке, и таким же кружком, раскрашенным против часовой стрелки. Их нетренированному мышлению кажется, по-видимому, что кружки одинаковы: они не то чтобы понимают, что кружки можно наложить перевернув, они просто не видят исходной разницы. Этим можно объяснить то, что даже «право-рукие» дети часто пишут наоборот печатные буквы и даже целые слова.

Может быть, ум наш потенциально более гибок, чем предполагал Кант. Наша неспособность четко представлять себе четырехмерные структуры вроде гиперкуба целиком может определяться тем фактом, что в человеческой памяти зарегистрирован только опыт, полученный в трехмерном мире. Может ли ребенок приучиться мыслить четырехмерными образами, если у него будут соответствующие игрушечные «учебные пособия»? Этот вопрос серьезно обсуждался некоторыми математиками, а в научно-фантастической литературе стал даже избитым.

А есть ли зеркальные отражения у гипертел 4-пространства? Да, эта двойственность существует на любом уровне. В одном измерении фигуры отражаются в точке, в двух измерениях — в линии, в трех измерениях — в плоскости. В четырехмерном мире отражение производится трехмерным телом и так далее для пространств еще более высоких размерностей. В каждом пространстве n -измерений «зеркалом» является «поверхность» с числом измерений n —1. В любом n -мерном пространстве асимметричную фигуру можно совместить с ее зеркальным изображением с помощью поворота в пространстве размерности n + 1. Может быть, наш гипотетический Кант XX столетия выразил бы это следующим образом: только «чистый разум» самого господа бога, который стоит над пространством и временем, видит, что пары энантиоморфных структур во всех пространствах идентичны и полностью наложимы друг на друга.