Маркос Санчес - Тайна за тремя стенами. Пифагор. Теорема Пифагора

Если соединить тремя отрезками квадраты при прямоугольном треугольнике, образуется шестиугольник, в котором

появятся три новых треугольника с площадями Т 1, Т 2и Т 3(см. рисунок 15). Каковы их площади? Во всех случаях их площади в точности равны площади исходного треугольника: Т 1= Т 2= Т 3= Т. На рисунке 16 показано, что Т = Т 1, так как у обоих треугольников одинаковы основание и высота. Для других треугольников также действительно это соотношение. Если взять любой произвольный треугольник АВС, то можно построить на его сторонах три квадрата и задать вопрос, каково соотношение площадей этих квадратов. Возьмем, к примеру, треугольник с острым углом (A < 90°). Решение показано на рисунке 17. На нем проведены три высоты треугольника. Эти высоты продолжены так, чтобы соответствующие прямые делили каждый квадрат, построенный на сторонах треугольника, на два прямоугольника. Подставляя длины сторон, получаем, что площадь верхнего правого прямоугольника равна с · (a cos В). Удивительно, что такова же и площадь нижнего правого прямоугольника. Площади секций слева равны b · (a cos С). Добавляем еще два сегмента с площадями b · (с cos А) и получаем результат:

a 2= b 2+ c 2- 2 · b · c · cosA,

по закону косинуса.

Таким образом, если А = 90°, cos 90°= 0, и мы получаем b 2+ с 2= а 2, известное пифагорово соотношение. Таким образом, закон косинуса — это продолжение теоремы Пифагора. Еще одно удивительное свойство проявляется, если построить четыре квадрата на сторонах параллелограмма. Как можно видеть на рисунке 18, сумма площадей этих квадратов равна сумме площадей двух квадратов, построенных на диагоналях параллелограмма.

Закончить описание современных областей применения одного из самых великих математических достижений в истории можно парой развлекательных задачек. Во-первых, теорема Пифагора позволяет ответить на вопрос, которым люди задавались с того момента, как узнали о кривизне земной поверхности: на каком расстоянии от нас находится видимый горизонт? Чтобы ответить, надо знать лишь высоту над уровнем моря, на которой находится наблюдатель. К примеру, если он стоит, озирая окрестности, на горе высотой 1000 м, можно применить нашу теорему следующим образом:

(R + h) 2= R 2+ v 2.

Следовательно:

v 2= (R+h) 2- R 2= (R 2+ 2Rh + h 2)- R2 = h 2+ 2Rh = h(h+2R),

где R — радиус Земли. Так как 2R + h ≈ 2R, поскольку h значительно меньше R, получается:

v 2≈ h(2R)

v ≈ √(2Rh).

И так как R = 6371 км, a h = 1 км, получаем:

v ≈ 112, 88 км.

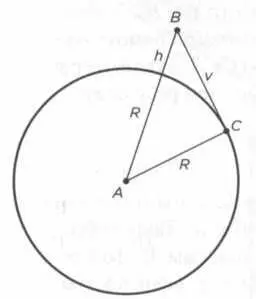
РИС. 19

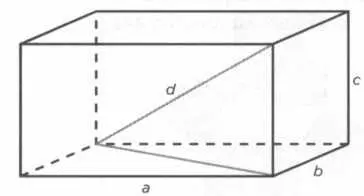
РИС. 20

И наконец, зная соотношение Пифагора как типичное свойство плоских прямоугольных треугольников, можем ли мы применить теорему к трехмерным фигурам? Да, сделать это можно разными способами. Известный и наиболее наглядный — выразить диагональ d коробки со сторонами a, b, с через теорему Пифагора: d 2= а 2+ b 2+ с 2(см. рисунок 20).

На пике греческой колонизации Пифагор попытался осуществить свой проект по созданию в Великой Греции утопического общества, построенного на духовных и философских основаниях. Он основал братство, в которое в равном количестве вошли мужчины и женщины. Члены братства имели разную степень доступа к магическо-математическим знаниям в соответствии со своим местом в иерархии.

Это первое сообщество такого типа, о котором мы знаем, — настоящее «братство числа».

Пифагорейство было способом жизни. Сообщество верных Пифагору подчинялось целому ряду правил, которые охватывали все аспекты повседневного бытия. Доступ к истине и спасению зависел от строгого выполнения норм, как это характерно для мистерических религий.

Основы этики сообщества определялись идеей бессмертия души, которая придавала всей жизни пифагорейцев характер религиозный и аскетический. Большинство предписаний были направлены на то, чтобы члены братства учились властвовать собой, отказывались от страстей и презирали телесные нужды — вот условия, необходимые для постижения высшего знания. В этом контексте музыка считалась «лекарством души» благодаря ее умиротворяющему действию, а высшей добродетелью становилась духовная гармония — состояние совершенства, которого возможно достичь лишь в следующих перерождениях. Математическая значимость чисел уже признавалась, но, по всей видимости, при жизни Пифагора концепция числа еще не оказывала такое влияние ни на этику братства, ни на космологию.

Для пифагорейцев жизнь имела мистическую цель — прикоснуться к божественному. Поэтому все их существование было организовано как восхождение по ступеням.

Так же как и в орфизме, адепты которого видели в человеке божественное начало и полагали главной целью жизни борьбу за его восстановление, Пифагор считал душу божественной частью человека и его единственной надеждой на спасение. Можно без колебаний квалифицировать школу, основанную самосским мудрецом, как секту. Особенности пифагорейской жизни, как мы их знаем из описаний историков, в точности соответствуют всем элементам, характерным для религиозной секты, если употреблять этот термин в социологическом смысле, без уничижительного оттенка. Учитель, обладающий наибольшим духовным авторитетом, предлагал своим последователям систему инициаций и обязательных правил поведения, включал их в иерархическую структуру разрядов и категорий и распределял их по ступеням восхождения к истине. Члены группы различались по одежде, питанию и ритуалам, которые они исполняли, — своего рода альтернативная по отношению к традиционной жизнь.

Пифагорейская иерархия соответствовала разным степеням инициации членов секты. Основное разделение было на две группы: акусматики и математики. Первые слушали наставления учителя, но не имели доступа к более полному изложению их оснований. Вторые, напротив, изучали вышеуказанные основания и были допущены к тайнам их истолкования. Эти загадочные наставления давались в весьма аллегорической форме и назывались акусматами, и посвященные первого уровня должны были заучивать их наизусть. Традиция говорит, что Пифагор заимствовал этот характерный для сект метод обучения в Египте, но достоверно известно, что пифагорейские максимы очень напоминали сентенции, получаемые от дельфийского оракула.

К этому самому общему, хорошо известному делению добавлялась разветвленная система ступеней посвящения, связанных с властью и соответствующих близости к вершинам логического знания. В свою очередь, степень внутренней власти в секте была связана с соблюдением суровых правил и еще более суровым образом жизни.