Маркос Санчес - Тайна за тремя стенами. Пифагор. Теорема Пифагора

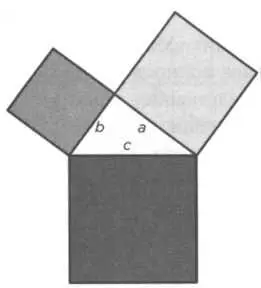
РИС. 6

РИС. 7

РИС. 8

РИС. 9

В противовес такому графическому доказательству, основанному на теории пропорций Пифагора, — теории несовершенной, так как она применима только к соизмеримым количествам, — некоторые историки математики выдвигают другое доказательство, алгебраического характера. Пифагор мог доказать теорему через подобие треугольников — на рисунке 9 треугольники АВС, АСН и СВН — с пропорциональными соответствующими сторонами. Возьмем треугольник АВС с прямым углом С, для которого отрезок СН представляет собой высоту, опущенную на гипотенузу, и делит ее на отрезки d и V — проекции, соответственно катетов а и b. Прямоугольные треугольники АВС, АСН и СВН имеют три общие стороны: каждый из треугольников имеет по две стороны, общие с другими, а их острые углы равны, так как они либо общие, либо составляют вместе прямой угол. Таким образом, треугольники подобны.

Подобие треугольников можно применить двумя способами.

— Подобие треугольников АВС и АСН: два треугольника подобны, когда два или более угла у них конгруэнтны (что доказал Евклид):

b/b' = c/b

b2 = b'c.

— Подобие треугольников АВС и СВН:

a/a' = c/a

a2 = a'c.

из чего вытекает так называемая теорема катета. Суммируем:

а 2+ b 2= а'с + b'с = с(а' + b'),

но (а' + b') = с, из чего следует

а 2+ b 2= с 2.

Евклид жил в Александрии около 300 года до н.э. и был автором «Начал» (Stoicheia) — труда, оказавшего огромное влияние на развитие математики и науки в целом. В этой книге он собрал все геометрические знания своей эпохи, не считая собственных доказательств, изложенных строго и изящно, включая определения, формулировки и общие сведения. Этот труд был не просто блестящим компендиумом, а серьезной работой по упорядочиванию геометрических знаний. Возможно, именно поэтому вплоть до последнего времени эта книга оставалась эталоном геометрического трактата. «Начала» занимают второе место по количеству изданий и переводов, уступая только Библии. К настоящему времени они выдержали более тысячи переизданий.

«Начала» делятся на 13 книг: четыре первые посвящены основам планиметрии — конгруэнтность треугольников, равенство площадей, золотое сечение, круг, правильные многоугольники, некоторые квадратуры и, естественно, теорема Пифагора (книга I, предложение 47). Свойства теоремы Пифагора используются в геометрическом контексте измерения площади фигур. Теорема Пифагора вновь упоминается в книге VI, а также в книге X, где речь идет о квадратных корнях.

В предложении 47 Евклид постулирует, что в квадратных треугольниках квадрат стороны, противоположной прямому углу, равен сумме квадратов сторон, прилегающих к нему. Иллюстрация к этому утверждению получила название «ветряной мельницы» (см. рисунок).

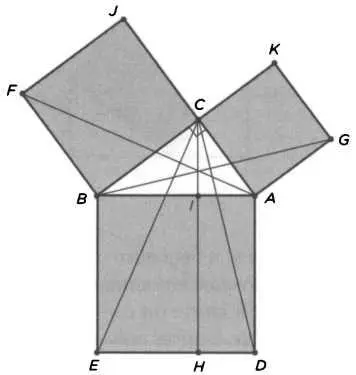
Доказательство выполняется с помощью расчета площадей. Оно заключается в том, чтобы доказать равенство треугольников BFA и ВСЕ и то, что их удвоенная площадь равна, с одной стороны, площади квадрата CBFJ, а с другой — площади прямоугольника ВШЕ. Таким же образом квадрат CKGA имеет ту же площадь, что и прямоугольник AIHD. Отсюда выводится теорема Пифагора, которую можно сформулировать следующим образом: площадь квадрата BADE равна сумме площадей квадратов CBFJ и CKGA.

Евклида считают отцом геометрии.

Хотя, по всей вероятности, ни один из результатов в «Началах» не является его открытием, нет сомнений, что именно Евклиду мы обязаны структурированием сведений и способом их изложения. О его жизни известно мало — почти исключительно те сведения, которые сообщает философ Прокл (V век) в своих комментариях к книге I «Начал».

По словам Прокла, Евклид родился ок. 325 года до н.э., жил и преподавал в Александрии и умер прибл. в 265 году до н.э. Кроме того, Прокл утверждает (и это выглядит весьма правдоподобным), что, судя по особенностям его работы, Евклид, возможно, обучался в школе Платона или у кого-то из его учеников. Таким образом, по сведениям Прокла, Евклид жил в эллинистический период. Это более вероятно, чем то, что он жил в классической Греции, учитывая, что в его книге есть отсылки к знаниям той эпохи. Так, Евклид сгруппировал описываемые им открытия способом, непохожим на то, как это делали греки классического времени. Тот же Прокл говорит, что Евклид собрал результаты философа и математика Евдокса (ок. 390-337 до н.э.) в области теории пропорций и математика Теэтета (ок. 417-369 до н.э.) в области правильных многоугольников и что в целом представил в своей книге неопровержимые доказательства множества теорем своих предшественников, о которых дошли лишь скудные сведения. Не сохранилось изначальной редакции труда самого Евклида, так что его тексты приходится реконструировать по комментариям и заметкам более поздних авторов, особенно византийских, латинских и арабских.

Евклид, занимающийся геометрией. С рельефа Андреа Пизано, XIV век (Музей Домского собора, Флоренция).

Теорема показывает также, как получить квадрат, по площади равный двум заданным квадратам, то есть как найти такое значение х, при котором х 2= а 2+ b 2, так что это еще один пример применения геометрической алгебры. Если предложение 47 представляет собой кульминацию первой книги «Начал», то еще более интересно, как впоследствии Евклид доказывает теорему, ей обратную. Это предложение 48, которому обычно уделяется не так много внимания, но которое имеет огромное логико-дедуктивное значение. В нем постулируется, что если в треугольнике квадрат одной из сторон равен сумме квадратов двух других, то угол, который образуют эти стороны, прямой (см. рисунок 10).

РИС. 10

Доказательство состоит в том, чтобы построить отрезок CD, перпендикулярный АС и равный СВ. Согласно заданным условиям: