Маркос Санчес - Тайна за тремя стенами. Пифагор. Теорема Пифагора

ВС 2+АС 2=АВ 2,

и, так как треугольник ADC прямоугольный,

АС 2+ CD 2=AD 2.

Поскольку ВС = CD, АВ 2= AD 2, то, следовательно, АВ = AD. Следовательно, треугольники ADC и АВС конгруэнтны, а угол АСВ, равный углу ACD, прямой.

Евклид приводит и графическое доказательство, где квадраты, выстроенные на катетах, превращаются в параллелограммы той же площади (так как они имеют то же основание и ту же высоту), а те, в свою очередь, трансформируются в квадрат, построенный на гипотенузе. Это гениальное доказательство представлено на рисунке 11.

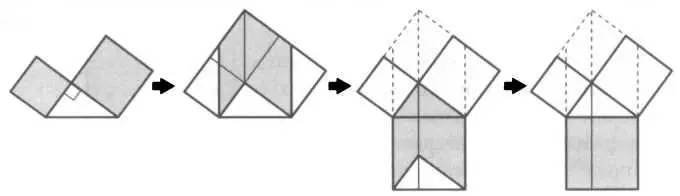
РИС. 11

Оксирннхский папирус 29, фрагмент «Начал», датированный II—IV веками (Филадельфия).

Фрагмент «Афинской школы» Рафаэля, Евклид изображен с циркулем. С противоположной стороны фрески находится Пифагор (Рим).

Теорема Пифагора числится среди имеющих наибольшее число возможных способов доказательства. Одно из объяснений этого явления в том, что в Средние века представление нового способа ее доказательства было одним из условий получения степени Magister matheseos, то есть магистра математики, и в известном смысле это умение стало со временем универсальным показателем общего образования человека.

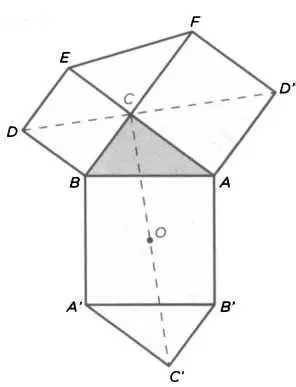
РИС. 12

Гениальный Леонардо да Винчи (1452-1519) был образцом универсального человека эпохи итальянского Возрождения, поскольку блестящим образом сочетал в себе знания в самых разных областях — как в сфере науки, так и искусства. Человек, который запечатлел таинственную красоту Джоконды и изобрел бесчисленные удивительные механизмы, смог представить собственное блестящее доказательство теоремы Пифагора. Леонардо основывался на знаменитой фигуре «мельницы», то есть треугольника с квадратами, построенными на трех его сторонах. К ним сверху он добавил треугольник ECF, а снизу разместил копию исходного треугольника А'С В' (см. рисунок 12). Проведя отрезки DD' и СС', служащие друг другу перпендикулярами, можно убедиться, что DD' делит верхний шестиугольник ABDEFD' на симметричные половины, которыми, если их развернуть друг относительно друга, можно полностью накрыть шестиугольник АСВА'С'В'. Следовательно, два квадрата, построенные на катетах, в сумме дают площадь, равную площади квадрата, построенного на гипотенузе.

Спустя два с половиной тысячелетия после открытия теорема Пифагора находит самые разные математические и научные способы применения. Это математическое достижение, оказавшееся, возможно, столь живучим благодаря своей простоте, сохраняет свою важность при вычислении длин, площадей и объемов разнообразных фигур. В квадрате со стороной х диагональ будет равна х√2; в прямоугольнике со сторонами х и у диагональ равна √(х 2+ у 2); в параллелограмме (например, в коробке из- под обуви) размерами х, у, z диагональ составит √(х 2+ у 2+ z 2); в конусе с высотой h и радиусом основания r образующая равняется √(h 2+ r 2)... и так можно продолжать очень долго.

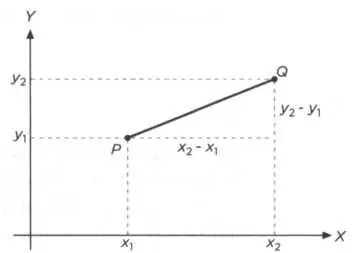
РИС. 13

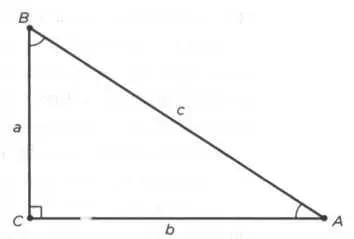
РИС. 14

Теорема Пифагора также лежит в основе декартовой системы координат на плоскости и в пространстве и позволяет определить расстояние d(P,Q) между двумя точками Р= (x 1,y 1) и Q= (х 2, у 2), как показано на рисунке 13. Применяя теорему, получаем:

Расстояние (P,Q) = √((x 2- x 1) 2+ (y 2- y 1) 2)·

В любом расчете, который предусматривает применение функций, проявляется пифагорово отношение, учитывая, что y = ƒ(x) в декартовом выражении. Теорема используется и в тригонометрии. С величинами углов прямоугольного треугольника связаны такие функции, как синус, косинус, тангенс... (см. рисунок 14), так что:

sin А = a/c cos А = b/c tg А = a/b.

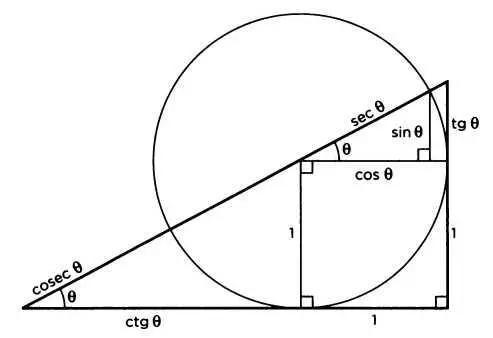
Таким образом, в тригонометрических терминах теорему Пифагора можно выразить как отношение sin 2А + cos 2А = 1. Теореме можно найти применение в топографии, картографии, навигации — морской или воздушной, — а также, конечно, в архитектуре, инженерном деле и во всех областях человеческой деятельности, где требуется расчет размеров. Чтобы показать исключительную важность теоремы в тригонометрии, можно привести следующий рисунок. Кроме того, что на нем мы видим круг и прямоугольный треугольник, катеты которого представляют собой синус и косинус, этот рисунок демонстрирует нам и многие другие величины, соответствующие большинству тригонометрических функций. Там можно найти тангенс, представляющий собой соотношение между синусом и косинусом, три взаимозависимых функции: секанс (то есть 1, деленное на косинус), косеканс (функция, обратная синусу) и котангенс (функция, обратная тангенсу). Таким образом, благодаря вездесущей теореме Пифагора приведенный на рисунке прямоугольный треугольник позволяет вывести очень много интересных соотношений, среди которых шесть тригонометрических функций.

tg 2θ +1 = sec 2θ,

ctg 2θ +1 = cosec 2θ,

(tg θ +1 ) 2+ (ctg θ +1 ) 2= (sec θ + cosec θ) 2.

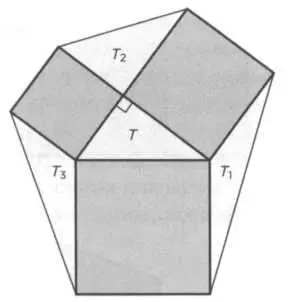
РИС. 15

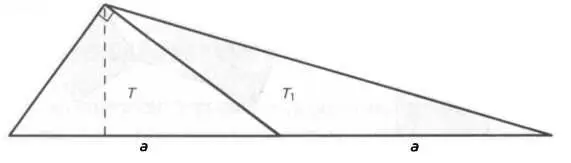
РИС. 16

Нет сомнений, что пифагорово соотношение тесно связано с конкретной геометрической фигурой — прямоугольным треугольником. Однако если принять во внимание классическое изображение этой теоремы в виде «ветряной мельницы», где три квадрата составлены так, что их стороны образуют катеты и гипотенузу прямоугольного треугольника, сами собой появляются некоторые вопросы. Что будет, если использовать квадраты для построения любого треугольника? Что будет, если они образуют параллелограмм?

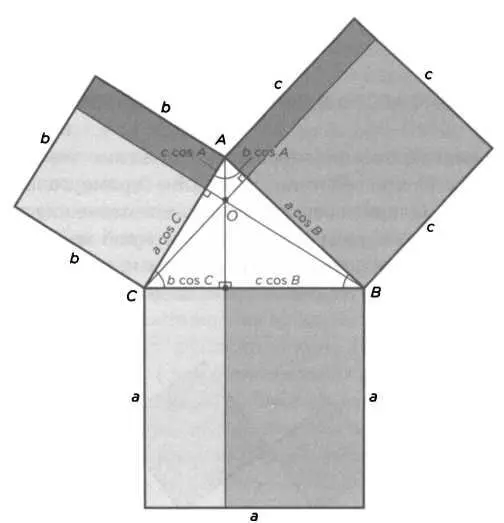
РИС. 17

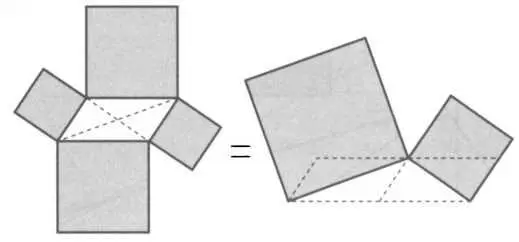
РИС. 18