Эдвард Шейнерман - Путеводитель для влюбленных в математику

Продолжим в том же духе и вычеркнем числа, делящиеся на 5, удалив таким образом пятую часть оставшихся чисел. Получится 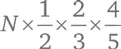чисел. Вот что останется:

1, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 49, 53, 59, 61, 67, 71, 73, 77, 79, …

Дальше мы вычеркиваем числа, делящиеся на 7, оставив шесть седьмых от нашего перечня, и будем двигаться по этому пути, пока не дойдем до числа P .

В конце концов количество тех чисел, которые мы не вычеркнули, станет равно

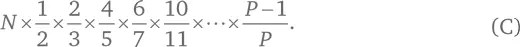
Так как все числа от 1 до N , кроме 1, делятся на какое-то простое число, выражение (C) должно быть равно 1. Верно? Вспомним, что N = 2 × 3 × 5 × 7 × 11 × 13 × … × P , подставим это произведение в выражение (C) и перегруппируем множители:

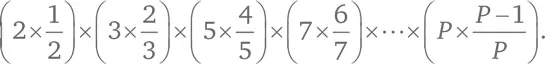
Это дает 1 × 2 × 4 × 6 × … × ( P – 1), что существенно больше 1! Выражение (C) должно быть равно 1, но очевидным образом не равно 1. Ошибка заключалась в изначальном предположении о том, что количество простых чисел конечно. Следовательно, их бесконечно много.

Есть много захватывающих вопросов о простых числах. Здесь я расскажу про две самые печально известные проблемы.

Хотя простых чисел бесконечно много, они встречаются все реже и реже, когда мы последовательно двигаемся от единицы к бесконечности. Позже (в главе 7) мы проанализируем среднюю разность между двумя соседними большими простыми числами. Однако простые числа все равно часто встречаются рядом, отличаясь на две и более единицы (единственная пара с отличием на один – 2 и 3). Если простые числа отличаются на две единицы, их называют простыми числами-близнецами , или парными простыми числами . Наименьшая пара близнецов – числа 3 и 5. Между 1 и 10 000 есть 205 пар близнецов, последние – числа 9929 и 9931.

Вопрос: простых чисел-близнецов бесконечно много?

Надо признать, что это неизвестно до сих пор.

Вот другой вопрос. Принято считать, что впервые его поставил немецкий математик Кристиан Гольдбах (1690–1764). Ему стало любопытно: какие четные числа (кроме 2) можно представить в качестве суммы двух простых? Вот пример:

Вопрос: можем ли мы продолжать этот ряд бесконечно? Гольдбах предположил, что любое четное число (за исключением 2) представляет собой сумму двух простых.

Но на самом деле мы до сих пор не знаем этого наверняка.

Изучение простых чисел относится к области математики под названием теория чисел . Британский математик Годфри Харди говорил: «До сих пор никто не обнаружил, как применить теорию чисел в военных целях».

Харди не мог предвидеть появления глобальной компьютерной сети и того факта, что безопасность в сети будет зависеть от простых чисел. Каким образом?

Пусть P и Q – два больших простых числа, скажем стозначных. Перемножить их – титанический труд для человека, но компьютер может посчитать произведение N = P × Q мгновенно. В то же время мы угодим в тупик, если попытаемся выяснить, какие два простых множителя дают N при умножении. Никто не знает эффективного алгоритма разложения таких огромных чисел на простые множители [25] Дадим зарок не пользоваться ничем, кроме карандаша и бумаги, и попробуем самостоятельно убедиться в том, что перемножать простые числа сравнительно легко, а раскладывать их произведение на множители – сложно. Для начала умножим 227 на 281. Если ни на что не отвлекаться, можно найти шестизначный ответ за пару минут. А теперь попробуйте найти без калькулятора два трехзначных простых множителя числа 211 591. Это не так-то просто. Ответ будет в конце главы. .

(Как это ни странно, определить, простое число или составное, можно достаточно быстро; однако найти простые множители больших чисел совсем не просто.)

Удивительно, однако эта диспропорция – легко перемножить, сложно разложить на множители – легла в основу создания шифров. Криптографическая система с открытым ключом [26] Термин «открытый ключ» означает, что раскрытие алгоритма шифрования – ключ к нему находится в открытом доступе – еще не рассекречивает сообщение. Один из таких алгоритмов изобрели в 1970-е Рон Ривест (Ron Rivest), Ади Шамир (Adi Shamir) и Леонард Адлеман (Leonard Adleman); по первым буквам их фамилий метод назвали RSA. устроена так, что можно раскрыть метод шифровки сообщений, но это не облегчит расшифровку засекреченных текстов. Мы не станем сейчас погружаться в детали метода, но основная идея состоит в том, что в процессе шифрования используется составное число N , представляющее собой произведение двух огромных простых чисел: N = P × Q. Расшифровка требует знания конкретных простых чисел P и Q . Если мы знаем N , этого достаточно для шифровки, но не для декодирования, а найти его простые множители все еще чрезвычайно сложно.

Мы используем криптографическую систему с открытым ключом всякий раз, когда совершаем покупки в интернете. Прежде чем браузер вышлет продавцу номер нашей кредитной карты, он получает от продавца открытый ключ шифрования. Браузер шифрует номер карты с помощью метода, о котором мы рассказывали. Если перехватить ключ, это ничего не даст, потому что метод шифровки не говорит о методе расшифровки (а его знает только продавец). Когда зашифрованное сообщение приходит на компьютер продавца, индивидуальный метод расшифровки раскрывает номер карты лишь законному получателю информации.

Криптографическая система с открытым ключом имеет и военные применения, вплоть до системы приведения в боевую готовность ядерного оружия [27] Криптографические системы на основе перемножения простых чисел будут эффективны лишь до тех пор, пока ученые не усовершенствуют квантовые компьютеры, где логические элементы (кубиты) могут находиться в состоянии 0 и 1 одновременно. Теоретически так называемый алгоритм Шора с помощью квантового компьютера способен разложить большое число на простые множители почти так же быстро, как происходит само шифрование. – Прим. пер. Несмотря на то что математики уже больше ста лет знают, что решение задачи о трисекции угла с помощью слепой линейки и циркуля невозможно, все время находятся энтузиасты, предлагающие очередное «решение». Анализ самых остроумных попыток можно найти в книге Андервуда Дадли «Смета трисекций» (A Budget of Trisections). Один из них равен – i , потому что (– i ) × (– i ) × (– i ) = (– i )³ = i . Но чему равны другие два? Ответ вы найдете в конце главы. .