Альфред Позаментье - Стратегии решения математических задач. Различные подходы к типовым задачам

Чтобы составить квадрат 1 × 1, требуется 4 зубочистки, как показано на рис. 2.3.

Чтобы составить квадрат 2 × 2, требуется 12 зубочисток (рис. 2.4).

Сколько потребуется зубочисток, чтобы составить квадрат 7 × 7?

Вы можете нарисовать квадрат 7 × 7 и просто подсчитать необходимое количество зубочисток. Такой подход вполне работоспособен, однако он громоздок и требует аккуратного построения чертежа.

Для начала попробуем построить несколько небольших квадратов и посмотрим, удастся ли нам выявить какую-либо закономерность. Нарисуем квадраты 3 × 3 и 4 × 4 (рис. 2.5 и 2.6).

Посмотрим теперь, что у нас получается.

Ну вот! При увеличении размера квадрата на 1 число необходимых зубочисток возрастает на 4. Продолжим таблицу:

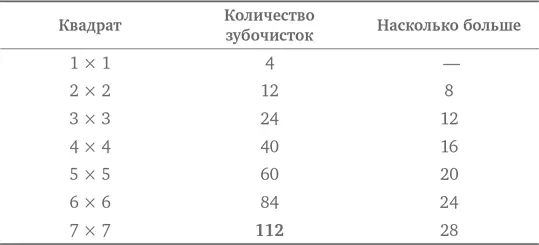
Таблица показывает, что числа в третьей колонке последовательно возрастают на 4. Количество зубочисток можно определить в обратном порядке, зная результат из третьей колонки. Для создания квадрата 7 × 7 необходимо 112 зубочисток.

Само название этой стратегии приводит в замешательство большинство людей. Такой подход совершенно неестественен. Когда мы ходили в школу, нас учили решать математические задачи в прямом порядке. Как бы то ни было, многие задачи в реальной жизни решаются именно от обратного. В качестве простого примера предположим, что вам нужно забрать ребенка с тренировки точно в 17:00. Во сколько нужно выйти из дома? Допустим, чтобы добраться до стадиона, нужно 30 минут. По-хорошему, к этому следует добавить запас 5 минут. Значит, выйти нужно за 35 минут, или не позднее 16:25. Даже не задумываясь об этом, мы использовали действие от обратного! Конечно, это сильно упрощенный пример применения данной стратегии.

Чтобы лучше понять такой тип мышления, рассмотрим еще один пример. Допустим, произошла автомобильная авария. Полиции приходится действовать от обратного, чтобы восстановить сцену произошедшего. Кто в кого врезался? Какой автомобиль занесло? Как далеко тянутся следы шин на асфальте? У кого было преимущество в проезде? Это всего лишь один из множества примеров действия от обратного.

В случае применения подхода от обратного мы обычно начинаем с конца задачи, или с «ответа». От этой точки восстанавливаются необходимые действия. Так, если в задаче говорится «увеличилось на 2», мы «уменьшаем на 2», или вычитаем 2. Как-никак, если мы увеличили что-то на 2, то для возврата к предыдущему этапу нужно уменьшить это на 2. Аналогичным образом, если говорится об умножении на 3, то в случае действия от обратного, необходимо разделить результат на 3. Рассмотрим типичную задачу.

Средний результат Марии в 11 тестах равен 80. При определении итогового среднего результата учительница проявляет благосклонность и отбрасывает низший результат. В нашем случае она отбрасывает 30. Какой итоговый средний результат у Марии?

Будем двигаться от среднего результата Марии. Среднее (или среднее арифметическое) обычно определяется путем сложения всех результатов и деления суммы на количество результатов. Если средний результат 11 тестов равен 80, то сумма результатов 11 тестов должна составлять 11 × 80 = 880. (Обратите внимание на то, что мы умножаем на 11, т. е. выполняем обратное действие по отношению к первоначальному делению на 11.) Вычтем результат 30, который учительница отбросила, и уменьшим количество тестов на единицу. Таким образом, суммарный результат 10 тестов равен 850. Итоговый средний результат Марии равен:

850: 10 = 85.

Попробуем решить еще одну задачу с помощью действия от обратного.

Дэвид вернулся после четырех раундов игры в бейсбольные карточки. В его набор теперь входят 45 карточек. Когда я поинтересовался его успехами, он ответил, что потерял половину карточек в первом раунде. Во втором раунде он выиграл в 12 раз больше того, что было у него в тот момент. В третьем раунде выигрыш составил 9 карточек. Четвертый раунд закончился вничью, поэтому количество карточек у игроков не изменилось. Сколько карточек было у Дэвида перед началом игры?

Можно, конечно, составить ряд уравнений и попробовать решить задачу напрямую. Однако давайте посмотрим, сработает ли здесь наш подход от обратного. У нас есть конечный результат (45 карточек), а найти нужно начальное количество. Это своего рода «товарный знак» типичной задачи, эффективно решаемой с помощью вычисления от обратного. Итак, Дэвид закончил игру с 45 карточками. Четвертый раунд закончился вничью, поэтому в конце третьего раунда у него были все те же 45 карточек. В третьем раунде выигрыш составил 9 карточек, значит в конце второго раунда количество карточек было равно 36. Во втором раунде мальчик выиграл в 12 раз больше карточек, чем было, поэтому в конце первого раунда он должен был иметь 3 карточки. В первом раунде Дэвид проиграл половину своих карточек, таким образом, он начал игру с 6 карточками. Подход от обратного позволил легко решить эту задачу.

Сумма двух чисел равна 2. Произведение этих же двух чисел равно 5. Найдите сумму обратных величин этих двух чисел.

Задача очевидно предполагает составление двух уравнений с двумя неизвестными:

x + y = 2;

xy = 5.

Эти два уравнения можно решить одновременно с использованием формулы корней квадратного уравнения: 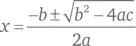для ax 2+ bx + c = 0. Однако этот метод дает значения для x и y в виде комплексных чисел, а именно 1 + 2 i и 1–2 i . В соответствии с условиями нашей задачи нам нужно найти сумму обратных величин этих двух квадратных корней.

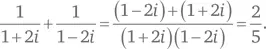
Подчеркнем, что в таком методе нет ничего неправильного, это просто не самый изящный способ решения задачи.