Альфред Позаментье - Стратегии решения математических задач. Различные подходы к типовым задачам
- Название:Стратегии решения математических задач. Различные подходы к типовым задачам
- Автор:
- Жанр:
- Издательство:Альпина Паблишер
- Год:2018
- Город:Москва
- ISBN:978-5-9614-5172-6
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Альфред Позаментье - Стратегии решения математических задач. Различные подходы к типовым задачам краткое содержание
В этой книге рассказывается о десяти различных стратегиях решения задач. Каждая глава начинается с описания конкретной стратегии и того, как ее можно использовать в бытовых ситуациях, а затем приводятся примеры применения такой стратегии в математике. Для каждой задачи авторы приводят сначала стандартное решение, а затем более элегантный и необычный метод. Так вы узнаете, насколько рассматриваемая стратегия облегчает поиск ответа.
Стратегии решения математических задач. Различные подходы к типовым задачам - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
Образцовое решение
Подход от обратного может оказаться полезным для решения этой задачи. А раз так, то начнем со следующих рассуждений.
В представленной ситуации есть два временных периода:
1. Нынешнее время, когда Марии 24 года.
2. Прошлое время n лет назад.
Введем следующие обозначения:
M — возраст Марии (24), A — возраст Анны, n — разница между двумя временными периодами.
В первом временном периоде — Мария в два раза старше, чем была Анна:
2 ( A − n ) = M . (3.1)
Во втором временном периоде — когда Марии было столько же, сколько Анне сейчас:
M − n = A . (3.2)
Подставим уравнение 3.2 в уравнение 3.1:
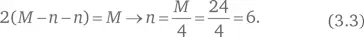
Значение n = 6 при подстановке в уравнение 3.2 дает:
M − 6 = A → A = 24 − 6 = 18.
Таким образом, возраст Анны составляет 18 лет.
Задача 3.6
От какой точки в выпуклом четырехугольнике сумма расстояний до каждой из вершин будет минимальной?
Обычный подход
Большинство без особых раздумий пытаются методом проб и ошибок найти точку, для которой сумма расстояний до вершин будет наименьшей. Вполне возможно, что кто-то выберет точку на пересечении диагоналей. Это правильный ответ, однако такой подход оставляет вопросы.
Образцовое решение
Наша стратегия поиска ответа от обратного оказывается более рациональной в данном случае. Возьмем четырехугольник ABCD с диагоналями, пересекающимися в точке E , и с точкой P , которая, на наш взгляд, может быть искомой, имеющей минимальную сумму расстояний до вершин. Соединим точку P пунктирными линиями с вершинами, как показано на рис. 3.5.
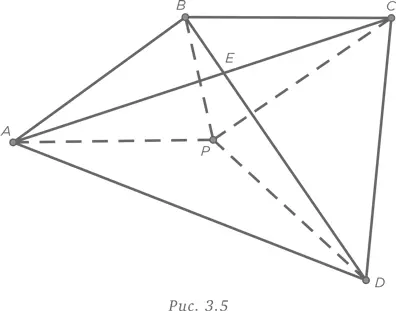
Рассмотрение треугольника APC показывает, что AP + PC > AC , поскольку сумма любых двух сторон треугольника всегда больше третьей стороны. Аналогичным образом, BP + PD > BD . В результате суммирования мы получаем, что AP + PC + BP + PD > AC + BD . Таким образом, отталкиваясь от предположения, что P может быть искомой точкой, мы находим, что выбор любой другой точки даст такой же результат. Единственной точкой, удовлетворяющей условиям задачи, является точка E на пересечении диагоналей.
Задача 3.7
Допустим, квадратные корни из уравнения x 2 + 3x — 3 = 0 равны r и s . Чему равна сумма r 2 + s 2 ?
Обычный подход
Обычный подход заключается в решении уравнения для значений r и s . Используя формулу 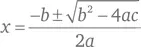 для определения корней квадратного уравнения вида ax 2+ bx + c = 0, мы получаем:
для определения корней квадратного уравнения вида ax 2+ bx + c = 0, мы получаем:
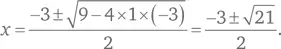
Теперь нам нужно найти квадраты этих корней и их сумму:
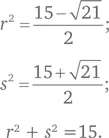
Образцовое решение
Чтобы получить более изящное решение, нужно вспомнить зависимость из элементарной алгебры, в соответствии с которой сумма корней квадратного уравнения ax 2+ bx + c = 0 составляет 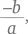 а произведение корней
а произведение корней 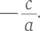 Из приведенного в условиях задачи уравнения мы находим, что сумма корней r + s = –3, а произведение rs = –3. При подходе от обратного, т. е. при определении суммы квадратов корней вместо прямых вычислений, как мы делали выше, для определения корней нам нужно искать эту сумму, поскольку ( r + s ) 2= r 2+ s 2+ 2 rs . Перепишем это уравнение следующим образом r 2 + s 2 = (r + s) 2 — 2rs .
Из приведенного в условиях задачи уравнения мы находим, что сумма корней r + s = –3, а произведение rs = –3. При подходе от обратного, т. е. при определении суммы квадратов корней вместо прямых вычислений, как мы делали выше, для определения корней нам нужно искать эту сумму, поскольку ( r + s ) 2= r 2+ s 2+ 2 rs . Перепишем это уравнение следующим образом r 2 + s 2 = (r + s) 2 — 2rs .
Таким образом, значение r 2 + s 2 = (–3) 2— 2 (–3) = 9 + 6 = 15.
Задача 3.8
Макс, Сэм и Джек играют в необычную карточную игру. В этой игре проигравший отдает другим игрокам столько денег, сколько у них есть. Макс проигрывает в первой партии и отдает Сэму и Джеку столько денег, сколько есть у каждого из них. Сэм проигрывает во второй партии и отдает Максу и Джеку столько денег, сколько есть у каждого из них. Джек проигрывает в третьей партии и отдает Максу и Сэму столько денег, сколько есть у каждого из них. На этом они решают закончить игру, и у каждого остается ровно $8,00. Сколько денег у каждого из игроков было перед началом игры?
Обычный подход
Задача предполагает составление ряда уравнений, представляющих каждую партию. Обозначим начальную сумму денег у каждого игрока следующим образом: Макс — x , Сэм — y , Джек — z .

В последней партии, как мы знаем, каждое из значений равно 8. Это дает следующие три уравнения с тремя неизвестными:

В результате решения системы из трех уравнений мы получаем:
x = 13, y = 7, z = 4.
Образцовое решение
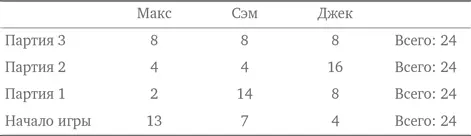
Обратите внимание, что в задаче дается конечная ситуация и спрашивается, какой была начальная ситуация. Это может указывать на эффективность подхода от обратного при решении. Также заметьте, что в соответствии с описанием ситуации в игре постоянно находится одно и то же количество денег (а именно $24). Подход от обратного дает изящное решение.
Макс начинает с $13, Сэм — с $7, а Джек — с $4. Ответ получился таким же, как и при обычном подходе, однако решение было более изящным.
Задача 3.9
Ал и Стив делят пятнистых саламандр для участия в выставке. Ал отбирает для своей экспозиции саламандр с двумя пятнами, а Стив — с семью пятнами. У Ала на пять саламандр больше, чем у Стива. Всего на их саламандрах 100 пятен. Сколько саламандр на двух экспозициях?
Обычный подход
Характер этой задачи создает сложности для использования алгебры. Обычно количество саламандр у Ала обозначают как x , а количество саламандр у Стива — как y . Это позволяет составить следующие уравнения:
x — y = 5;
2 x + 7 y = 100.
Для решения этих двух уравнений умножим первое из них на 2:
Читать дальшеИнтервал:
Закладка:










