Альфред Позаментье - Стратегии решения математических задач. Различные подходы к типовым задачам
- Название:Стратегии решения математических задач. Различные подходы к типовым задачам
- Автор:
- Жанр:
- Издательство:Альпина Паблишер
- Год:2018
- Город:Москва
- ISBN:978-5-9614-5172-6
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Альфред Позаментье - Стратегии решения математических задач. Различные подходы к типовым задачам краткое содержание
В этой книге рассказывается о десяти различных стратегиях решения задач. Каждая глава начинается с описания конкретной стратегии и того, как ее можно использовать в бытовых ситуациях, а затем приводятся примеры применения такой стратегии в математике. Для каждой задачи авторы приводят сначала стандартное решение, а затем более элегантный и необычный метод. Так вы узнаете, насколько рассматриваемая стратегия облегчает поиск ответа.
Стратегии решения математических задач. Различные подходы к типовым задачам - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
Задачу также можно решить, посмотрев на нее с другой точки зрения. Четырехугольник с тремя прямыми углами является прямоугольником. Отрезок AB — диагональ прямоугольника. PO также диагональ прямоугольника. Поскольку диагонали прямоугольника равны, радиус круга PO = 12, а площадь круга равна 144 π .
Задача 4.2
Стандартную колоду из 52 игральных карт делят случайным образом на две стопки по 26 карт в каждой. Как количество красных карт в одной стопке соотносится с количеством черных карт в другой?
Обычный подход
При решении этой задачи, как правило, количество черных и красных карт в каждой стопке представляют следующим образом:
B1 = количество черных карт в стопке 1;
B2 = количество черных карт в стопке 2;
R1 = количество красных карт в стопке 1;
R2 = количество красных карт в стопке 2.
Поскольку общее количество черных карт равно 26, можно записать, что B1 + B2 = 26, а поскольку общее количество карт в стопке 2 равно 26, мы получаем R2 + B2 = 26.
Вычитание второго уравнения из первого, дает: B1 — R2 = 0. Таким образом, B1 = R2, т. е. количество красных карт в одной стопке равно количеству черных карт в другой. Хотя такое решение дает ответ, назвать его изящным нельзя. Наша цель в этой главе — найти такое решение, которое демонстрирует красоту и силу математики.
Образцовое решение
В качестве альтернативы возьмем все красные карты из стопки 1 и обменяем их на черные карты из стопки 2. Теперь все черные карты находятся в одной стопке, а красные — в другой. Таким образом, количество красных карт в одной стопке и количество черных карт в другой стопке должны быть равными. Задачу позволяет решить простая логика — нужно лишь взглянуть на эту задачу с другой точки зрения.
Задача 4.3
Лоэнгрину дали четыре отрезка цепи (рис. 4.2), в каждом из которых три звена. Покажите, как соединить эти четыре отрезка в замкнутую цепь, разомкнув и сомкнув не более трех звеньев.
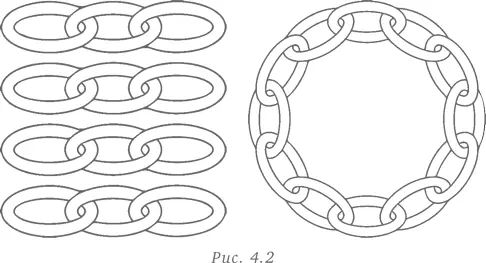
Обычный подход
Обычно сначала пытаются разомкнуть последнее звено одного отрезка, присоединить его к другому отрезку и получить цепь из 6 звеньев. Затем размыкают звено третьего отрезка и присоединяют его к 6-звенной цепи, получая 9-звенную цепь. Присоединив последний отрезок к 9-звенной цепи, получают 12-звенную цепь, которая, однако, не является замкнутой . Таким образом, традиционный подход обычно завершается неудачей. Некоторые пробуют другие комбинации размыкания/замыкания звеньев каждого отрезка цепи, однако такой подход не приносит желаемого результата.
Образцовое решение
Эта задача хорошо решается с помощью стратегии принятия другой точки зрения. Можно даже сказать, что такой подход просто неоценим в данном случае. Вместо того, чтобы пытаться разомкнуть и замкнуть однозвено на каждом отрезке цепи , другая точка зрения предполагает размыкание всехзвеньев одного отрезка цепи и использование этих звеньев для соединения трех оставшихся отрезков цепи и получения требуемой замкнутой цепи. Это быстро приводит к правильному решению.
Задача 4.4
Какие натуральные числа менее 100 дают остаток 3 при делении на 7 и остаток 4 при делении на 5?
Обычный подход
Рассмотрим ряд натуральных чисел менее 100, которые дают остаток 3 при делении на 7: {3, 10, 17, 24, 31, 38, 45, 52, 59, 66, 73, 80, 87, 49}. Теперь рассмотрим ряд натуральных чисел менее 100, которые дают остаток 4 при делении на 5: {4, 9, 14, 19, 24, 29, 34, 39, 44, 49, 54, 59, 64, 69, 74, 79, 84, 89, 94, 99}.
Сравнив эти два ряда, находим три совпадающих числа: 24, 59 и 94.
Образцовое решение
Попробуем взглянуть на эту задачу с другой точки зрения. Искомые числа должны иметь форму 7 n + 3, а также форму 5 k + 4, где n и k — целочисленные неизвестные. Объединим эти величины так, чтобы искать числа в форме 35 r + p , где r и p — целочисленные неизвестные. Первый ряд чисел, имеющих форму 7 n + 3, также можно представить, как 35 r + 3, 35 r + 10, 35 r + 17, 35 r + 24 и 35 r + 31. Только одно из этих чисел имеет также форму 5 k + 4, а именно 35 r + 24. Для того, чтобы узнать, какие числа менее 100, удовлетворяют этому соотношению, зададим r = 0, 1 и 2 и получим три искомых числа: 24, 59 и 94.
Задача 4.5
Какое из следующих двух выражений больше, √5 + √8 или √4 + √10
Обычный подход
Учитывая нынешнее распространение калькуляторов, не удивительно, что люди обычно извлекают квадратный корень из каждого числа, затем определяют их суммы и получают требуемый ответ. Хотя такой подход довольно эффективен, его, конечно, не назовешь изящным.
Образцовое решение
Взглянем на задачу с другой точки зрения, а именно возведем в квадрат каждую из этих сумм и посмотрим, каким будет результат.
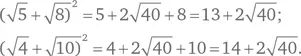
Упростив, таким образом, условия, мы видим, что сумма является большей из двух величин.
Задача 4.6
Чему равны все положительные целочисленные значения переменной n , для которой дробь 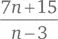 также является целым числом?
также является целым числом?
Обычный подход
Первой реакцией на эту задачу является попытка подставить разные значения n и посмотреть, какой результат будет целым числом. Например, если принять n = 4, мы получим 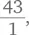 т. е. целое число. Хотя такой подход и позволяет выявить некоторые значения n , очень трудно сказать, все ли значения найдены. В результате обычно получается неполный ответ.
т. е. целое число. Хотя такой подход и позволяет выявить некоторые значения n , очень трудно сказать, все ли значения найдены. В результате обычно получается неполный ответ.
Образцовое решение
Воспользуемся стратегией принятия другой точки зрения. Для начала выполним деление:
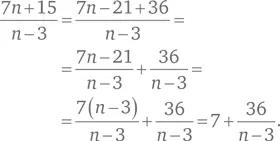
Чтобы эта величина была целым числом, n — 3 должно быть пропорционально 36. Делителями для числа 36 являются 1, 2, 3, 4, 6, 9, 12, 18 и 36. Таким образом:
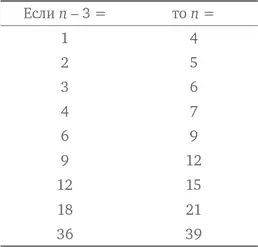
Значения n , при которых 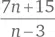 является целым числом, равны 4, 5, 6, 7, 9, 12, 15, 21 и 39.
является целым числом, равны 4, 5, 6, 7, 9, 12, 15, 21 и 39.
Задача 4.7
Каждый из 10 придворных ювелиров дает королевскому советнику г-ну Саксу стопку золотых монет. В каждой стопке находится 10 монет. Полноценные монеты весят 1 унцию. Однако в одной из стопок находятся «неполновесные» монеты, каждая из которых весит на 0,1 унции меньше. Г-н Сакс хочет выявить ювелира-жулика и стопку неполновесных монет с помощью всего лишь одного взвешивания. Как это сделать?
Читать дальшеИнтервал:
Закладка:










