Авинаш Диксит - Стратегические игры

Мы предоставляем вам возможность построить для этого случая график, аналогичный представленному на рис. 12.7. Для этого вам понадобится определить динамику, в соответствии с которой доли каждого типа в популяции сходятся к устойчивой равновесной комбинации.

Вспомните рассчитанную в разделе 6.Аравновесную смешанную стратегию в рациональной игре, где p = V/C — вероятность выбора стратегии «ястреб», а (1 — p ) — вероятность выбора стратегии «голубь». Есть ли параллель в эволюционной версии игры, когда фенотип выбрал бы смешанную стратегию? Проанализируем такую возможность. У нас по-прежнему есть игроки типа Я, использующие чистую стратегию «ястреб», и игроки типа Г, использующие чистую стратегию «голубь». Но теперь может существовать еще и третий фенотип С, применяющий смешанную стратегию, включая в нее стратегию «ястреб» с вероятностью p = V/C и стратегию «голубь» с вероятностью 1 — p = 1 — ( V/C ) = ( C–V )/ C .

Когда Я или Г встречает С, их ожидаемый выигрыш зависит от p — вероятности того, что С выберет стратегию Я, и от (1 — p ) — вероятности того, что С выберет стратегию Г. Тогда каждый игрок получает p , умноженное на его выигрыш в игре против Я, плюс (1 — p ), умноженное на его выигрыш в игре против Г. Таким образом, когда Я противостоит С, его ожидаемый выигрыш составит

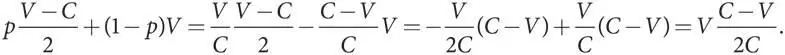
А когда Г противостоит С, его выигрыш равен

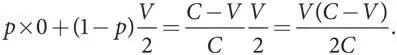
Уровни приспособленности двух типов одинаковы. Это не должно стать неожиданностью: соотношение чистых стратегий должно обеспечивать именно такое равенство. Тогда игрок типа С в противостоянии с другим игроком типа С получит тот же ожидаемый выигрыш. Для того чтобы было проще ссылаться на него в дальнейшем, обозначим его символом K , где K = V ( C–V )/2 C .

Но такое равенство создает проблему при проверке стратегии С на эволюционную устойчивость. Предположим, популяция целиком состоит из игроков типа С и в нее вторгаются мутанты типа Я, составляющие совсем малую долю h от общей численности популяции. Тогда типичный мутант получит ожидаемый выигрыш h ( V–C )/2 + (1 — h ) K . Для того чтобы вычислить ожидаемый выигрыш игрока типа С, необходимо учесть, что он противостоит другому игроку типа С в (1 — h ) случаях и каждый раз получает выигрыш K . Далее он вступает в противостояние с игроком типа Я в h взаимодействиях и в их ходе использует стратегию Я в p случаях и получает выигрыш ( V–C )/2 и стратегию Г в (1 — p ) случаев и получает выигрыш 0. Таким образом, общий ожидаемый выигрыш (уровень приспособленности) игрока типа С составляет

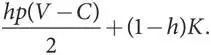
Поскольку у h очень малое значение, приспособленность игроков типа С и мутантов типа Я почти эквивалентна. Дело в том, что, когда мутантов очень мало, игроки как типа Я, так и типа С в основном противостоят только игрокам типа С и, как мы только что выяснили, в этом взаимодействии у обоих типов одинаковый уровень приспособленности.

Эволюционная устойчивость зависит от того, будет ли исходная популяция типа С более приспособленной, чем мутант типа Я, когда каждый из них противостоит одному из немногочисленных мутантов. В алгебраической форме тип С более приспособлен, чем тип Я, в противоборстве с другими мутантами типа Я, когда pV ( C–V )/2 C = pK > ( V–C )/2. В нашем примере это условие выполняется, так как V < C, то есть ( V–C ) имеет отрицательное значение, а K имеет положительное значение. На интуитивном уровне это условие говорит нам о том, что мутант типа Я всегда будет получать более низкие результаты в противостоянии с другим мутантом типа Я из-за высоких издержек в связи с дракой, но тип С вступает в драку только иногда, а значит, несет такие издержки лишь в p случаях. В целом тип С добивается большего в противостоянии с мутантами.

Аналогично успех вторжения типа Г в популяцию С зависит от сравнения уровня приспособленности мутанта типа Г с уровнем приспособленности мутанта типа С. Как и раньше, мутант противостоит другому игроку типа Г в d случаях, а игроку типа С в (1 — d ) случаях. Тип С также противостоит другому игроку типа С в (1 — d ) случаях, однако в d случаях С противостоит Г и использует стратегию Я в p из этих случаев, получая при этом выигрыш pV , а также применяет стратегию Г в (1 — p ) случаях, получая при этом выигрыш (1 — p ) V /2. Из этого следует, что уровень приспособленности типа «голубь» составляет [ dV /2 + (1 — d ) K ], тогда как уровень приспособленности типа С равен d × [ pV+ (1 — p ) V /2] + (1 — d) K. Последние члены выражений, описывающих уровни приспособленности, идентичны, а значит, вторжение «голубей» может быть успешным, только если V /2 больше pV + (1 — p ) V /2. Это условие не выполняется: последнее выражение содержит взвешенное среднее V и V /2, которое больше V /2 при V > 0. Таким образом, вторжение мутантов типа «голубь» не может завершиться успехом.

Этот анализ говорит о том, что С — эволюционно устойчивая стратегия. Следовательно, если V < C , популяция может продемонстрировать любой из двух эволюционно устойчивых исходов. Один подразумевает смешение типов (устойчивый полиморфизм), а другой — присутствие в популяции только одного типа, смешивающего стратегии в том же соотношении, которое определяет полиморфизм.

Теперь обобщим идеи, представленные в данном разделе, чтобы получить теоретическую основу и набор инструментов для дальнейшего использования. Такое обобщение неизбежно требует несколько более абстрактных обозначений и немного алгебры. В связи с этим мы рассмотрим только мономорфные равновесия в одном виде. Читатели, которые владеют математикой на должном уровне, смогут по аналогии описать полиморфные случаи с двумя видами. Читатели, которые не готовы к восприятию данного материала или для них он не представляет интереса, могут пропустить этот раздел без ущерба для целостности изложения материала [222].

Проанализируем взаимодействие между случайно отобранными из одного вида парами, популяции которого доступны стратегии I, J, K, …, среди которых могут быть как чистые, так и смешанные. Каждый отдельный член популяции запрограммирован на использование только одной из этих стратегий. Обозначим E (I, J) выигрыш игрока I от одного взаимодействия с игроком J. Выигрыш игрока I в противостоянии с другим представителем своего типа составляет E (I, I) в той же системе обозначений. Пусть W (I) — уровень приспособленности игрока I. Это просто его ожидаемый выигрыш в противостоянии с произвольно выбранными соперниками, когда вероятность встретить игрока определенного типа равна доле этого типа в популяции.