Авинаш Диксит - Стратегические игры
- Название:Стратегические игры
- Автор:
- Жанр:
- Издательство:Манн, Иванов и Фербер
- Год:2017
- Город:Москва
- ISBN:9785001008132
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Авинаш Диксит - Стратегические игры краткое содержание
Книга будет полезна как интересующимся математикой и ее применением в бизнесе и в жизни, так и тем, кто хочет развить стратегическое мышление и научиться принимать обоснованные решения.
Стратегические игры - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
Рис. 12.13.Таблица выигрышей для игры «ястреб — голубь»
Анализ этой игры аналогичен анализу дилеммы заключенных и игры в труса, только в ней числовые выигрыши заменены алгебраическими символами. Мы сопоставим равновесия в этой игре, когда игроки рационально выбирают стратегию «ястреб» или «голубь», после чего сравним исходы игры, когда игроки действуют автоматически, а успех вознаграждается более быстрым воспроизводством.
А. Рациональный стратегический выбор и равновесие1. Если V > C , то это дилемма заключенных, в которой стратегия «ястреб» соответствует стратегии «отказ от сотрудничества», а стратегия «голубь» — стратегии «сотрудничать». Стратегия «ястреб» — доминирующая для каждого игрока, но комбинация стратегий «голубь»/«голубь» — более благоприятный исход для обоих игроков.
2. Если V < C , тогда это игра в труса. Теперь ( V–C )/2 < 0, а значит, «ястреб» больше не доминирующая стратегия. В игре два равновесия Нэша в чистых стратегиях: «ястреб»/«голубь» и «голубь»/«ястреб». В игре также есть равновесие в смешанных стратегиях, при котором вероятность p выбора игроком Б стратегии «ястреб» имеет такое значение, которое поддерживает безразличие игрока А в отношении выбора стратегий:
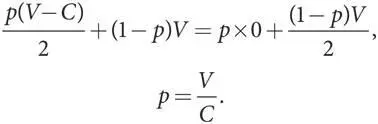 Б. Эволюционная устойчивость при V > C
Б. Эволюционная устойчивость при V > C
Начнем с популяции, состоящей преимущественно из «ястребов», и проверим, могут ли ее захватить мутанты типа «голубь». Придерживаясь условных обозначений для подобных игр, мы могли бы выразить долю мутантного фенотипа в популяции как m (от слова «mutant»), но для ясности будем использовать для мутанта типа «голубь» обозначение d (от «dove»). Таким образом, доля «ястребов» в популяции составляет (1 — d ). Тогда в противостоянии со случайно выбранным соперником «ястреб» будет встречаться с «голубем» в d случаях и получит V в каждом из них, а также встретится с другим «ястребом» в (1 — d ) случаях и получит ( V–C )/2 в каждом. Следовательно, уровень приспособленности «ястреба» равен [ dV + (1 — d )( V–C )/2]. Аналогичным образом уровень приспособленности одного из мутантов типа «голубь» составляет [ d ( V /2) + (1 — d )×0]. Поскольку V > C , отсюда следует, что ( V–C )/2 > 0. Кроме того, V > 0 подразумевает, что V > V/2. В таком случае при любом значении d от 0 до 1 имеем
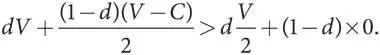
Стало быть, у «ястреба» более высокий уровень приспособленности, поэтому мутанты типа «голубь» не могут захватить популяцию. Стратегия «ястреб» эволюционно устойчива, а популяция мономорфна (все «ястребы»).
То же самое верно и для любой доли «голубей» в популяции при всех значениях d . Следовательно, какой бы ни была исходная комбинация типов, доля «ястребов» будет расти и они будут доминировать. Кроме того, если исходная популяция состоит только из «голубей», мутанты типа «ястреб» могут ее захватить. Таким образом, эта динамика говорит о том, что «ястреб» — единственная эволюционно устойчивая стратегия. Данный алгебраический анализ подтверждает и обобщает сделанный ранее вывод в числовом примере дилеммы заключенных в контексте игры в ценообразование (см. рис. 12.1).
В. Эволюционная устойчивость при V < CЕсли исходная популяция преимущественно «ястребы» с небольшой долей d мутантов типа «голубь», то у каждого из них такая же функция уровня приспособленности, как и функции, выведенные в разделе 6.Б. Однако когда V < C , ( V–C )/2 < 0. Мы по-прежнему имеем V > 0, а значит, V > V/2. Но поскольку значение d очень маленькое, сравнение этих членов с (1 — d ) играет гораздо более важную роль, чем сравнение с d , поэтому
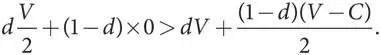
Следовательно, уровень приспособленности мутантов типа «голубь» выше уровня приспособленности доминирующего типа «ястреб», поэтому мутанты типа «голубь» могут захватить популяцию.
Однако если исходная популяция почти полностью состоит из «голубей», мы должны проанализировать, может ли небольшая доля h мутантов типа «ястреб» захватить ее. (Обратите внимание, что, поскольку мутант теперь относится к типу «ястреб», мы использовали символ h (hawk) для обозначения доли мутантов-захватчиков.) Уровень приспособленности мутантов типа «ястреб» [ h ( V–C )/2 + (1 — h ) V ] сопоставим c [ h × 0 + (1 — h )( V /2)] в случае мутантов типа «голубь». И снова V < C подразумевает, что ( V–C )/2 < 0, а V > 0 подразумевает, что V > V/2 . Но когда значение h небольшое, получаем
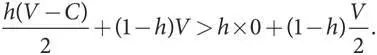
Это неравенство показывает, что уровень приспособленности «ястребов» выше, поэтому они захватят популяцию «голубей». Таким образом, мутанты каждого типа могут захватить популяцию другого типа. Поэтому она не может быть мономорфной и ни один чистый фенотип не может быть эволюционно устойчивой стратегией. Алгебраические расчеты снова подтверждают сделанный ранее вывод в числовом примере дилеммы заключенных в контексте игры в труса (см. рис. 12.6и рис. 12.7).
А что происходит в популяции, когда V < C ? Существуют два сценария. В первом каждый игрок придерживается чистой стратегии, но в популяции наблюдается устойчивая комбинация игроков, использующих разные стратегии. Это полиморфное равновесие, сформировавшееся в игре в труса, о которой шла речь в разделе 3. Второй сводится к применению каждым игроком смешанной стратегии. Мы начнем с полиморфного случая.
Г. V < C : устойчивая полиморфная популяцияКогда доля «ястребов» в популяции равна h , уровень их приспособленности составляет h ( V–C )/2 + (1 — h ) V , а уровень приспособленности «голубя» — h × 0 + (1 — h )( V /2). Уровень приспособленности «ястреба» выше, если
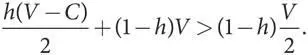
Это неравенство можно упростить:
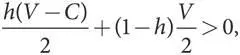
V — hC > 0,
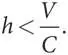
В таком случае уровень приспособленности типа «голубь» выше, когда h > V/C , или когда (1 — h ) < 1 — ( V/C ) = ( C–V )/ C . Стало быть, каждый тип более приспособлен, если его численность меньше. Следовательно, мы имеем устойчивое полиморфное равновесие в равновесной точке, в которой доля «ястребов» в популяции составляет h = V/C . Это и есть рассчитанная в разделе 6.Авероятность, с которой каждый отдельный игрок выбирает стратегию «ястреб» в равновесии Нэша в смешанных стратегиях данной игры при условии рационального поведения игроков. К тому же мы также получили эволюционное «обоснование» исхода в виде смешанной стратегии в игре в труса.
Читать дальшеИнтервал:
Закладка:










