Авинаш Диксит - Стратегические игры

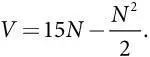
Стоимость строительства одной полосы, в том числе вознаграждение в размере нормальной прибыли, могло бы составить либо 3, либо 5 миллиардов долларов в зависимости от типа грунта на строительном участке. На данный момент будем считать, что правительство штата может определить объем затрат на строительство так же, как и подрядчик. В итоге оно выбирает количество полос N и составляет контракт таким образом, чтобы максимально увеличить выгоду для штата ( V ) за вычетом вознаграждения подрядчику (назовем его F ), то есть цель правительства штата — максимизировать свою чистую выгоду G , где G = V — F .

Допустим, властям штата известно, что фактический объем затрат составляет 3 (миллиарда долларов на одну полосу автомагистрали), следовательно, подрядчику придется выплатить 3 N за строительство автомагистрали, состоящей из N полос. Далее правительство выбирает такое значение N , которое обеспечивает чистую выгоду G согласно следующей формуле:

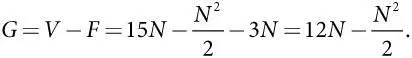
В приложении к главе 5мы вывели формулу поиска значения для максимизации функции этого вида. В частности, максимум функции

Y = A + BX − CX 2

будет при X = B/ (2 C ). В данном примере Y — это G, X — это N, A = 0, B = 12, C = 1/2. Применив формулу решения задачи максимизации, получим оптимальный выбор правительством штата значения N = 12(2 × 1/2) = 12. Следовательно, наиболее целесообразно выбрать автомагистраль на 12 полос, стоимость которой составит 36 миллиардов долларов. Таким образом, правительство предложит следующий контракт: «Мы заплатим 36 миллиардов долларов за строительство 12-полосной автомагистрали» [239]. Эта цена включает в себя нормальную прибыль, поэтому подрядчик охотно его подпишет

Аналогичным образом, если затраты составляют 5 миллиардов долларов в расчете на одну полосу, оптимальным значением N будет 10. Правительство предложит контракт на 50 миллиардов долларов за строительство 10-полосной автомагистрали. И подрядчик примет это предложение.

Теперь представим, что подрядчик знает, как оценить физические условия соответствующей местности, для того чтобы определить объем затрат на одну полосу автомагистрали, а правительство нет; оно может дать лишь приблизительную оценку этих затрат. Будем считать, что, по мнению правительства, объем затрат составит 3 (миллиарда долларов на одну полосу) с вероятностью 2/3 и 5 с вероятностью 1/3.

Что если правительство попытается добиться идеального оптимума и предложит подрядчику два контракта: «12-полосная автомагистраль за 36 миллиардов долларов» и «10-полосная автомагистраль за 50 миллиардов долларов»? Если объем затрат действительно составляет 3 миллиарда долларов в расчете на одну полосу, подрядчик получит больше прибыли, заключив второй контракт, хотя он и предназначен для ситуации, в которой объем затрат равен 5 миллиардов долларов на одну полосу. Истинная стоимость 10-полосной автомагистрали составит при этом 30 миллиардов долларов, и подрядчик заработает 20 миллиардов долларов сверхприбыли [240].

Такой исход нельзя назвать удовлетворительным. Предложенные контракты не предоставляют подрядчику достаточно сильного стимула выбирать между ними на основании объема затрат: он всегда будет отдавать предпочтение контракту на 50 миллиардов долларов. У правительства должен быть более приемлемый способ создания системы заключения контрактов на закупку.

Поэтому допустим, что правительство может разработать более общий механизм, обеспечивающий разделение типов проектов. Скажем, оно предложит подрядчику два контракта: «Контракт L: мы заплатим вам R Lдолларов за строительство N L полос» и «Контракт H: мы заплатим вам R Hдолларов за строительство N H полос». Если контракты L и H составлены правильно, при низком уровне затрат (3 миллиарда долларов на одну полосу) подрядчик выберет контракт L («low» — низкие затраты); при высоком (5 миллиардов долларов на одну полосу) — контракт H («high» — высокие затраты). Для того чтобы этот механизм скрининга работал, нужно, чтобы показатели, которые обозначены символами N L, R L, N H, R H, удовлетворяли определенным условиям.

Во-первых, по каждому контракту подрядчик, который несет соответствующие затраты (низкие при контракте L и высокие при контракте H), должен получить сумму (включающую нормальную прибыль), достаточную для покрытия его расходов. Иначе он не согласится с такими условиями и не станет заключать контракт. Следовательно, контракт должен удовлетворять двум ограничениям участия : 3N L≤ R Lдля подрядчика, когда объем затрат составляет 3, и 5N H≤ R Hдля подрядчика, когда объем затрат равен 5.

Кроме того, правительству необходимо составить такие два контракта, чтобы подрядчик, зная, что у него будет низкий уровень затрат, не получил выгоду, заключив контракт H и наоборот. Иначе говоря, эти контракты должны также удовлетворять двум ограничениям совместимости стимулов . Например, если истинные затраты низкие, контракт L обеспечит подрядчику сверхприбыль R L — 3N L, тогда как контракт H обеспечит сверхприбыль R H — 3N H. (Обратите внимание, что в последнем выражении количество полос и оплата те же, что и для контракта H, однако затраты подрядчика по-прежнему составляют 3, а не 5.) Для того чтобы удовлетворять ограничению совместимости при низком уровне затрат, контракты должны обеспечивать такое значение второго выражения, которое бы не превышало значение первого выражения. Следовательно, необходимо, чтобы R L — 3N L ≥ R H — 3N H. Точно так же, если истинные затраты низкие, сверхприбыль подрядчика в случае контракта L не должна превышать его сверхприбыли от контракта H. Стало быть, чтобы контракты удовлетворяли ограничению совместимости стимулов, нужно, чтобы R H — 5N H ≥ R L — 5N L.

Правительство стремится максимизировать чистую ожидаемую общественную выгоду от оплаты услуг подрядчика, поэтому использует вероятности этих двух типов в качестве весовых коэффициентов для вычисления математического ожидания. Таким образом, цель правительства — максимизировать функцию

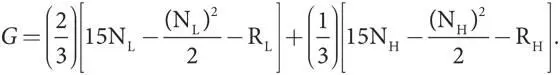
На первый взгляд может показаться, что это очень сложная задача с четырьмя переменными выбора и четырьмя ограничениями в виде неравенства. Однако ее можно существенно упростить, поскольку два ограничения являются избыточными, а оставшиеся два должны быть представлены в виде строгих равенств, что позволит нам подставить полученные выражения в уравнение вместо двух переменных.