Авинаш Диксит - Стратегические игры

Обратите внимание, что если ограничение участия при высоком уровне затрат 5N H ≤ R H, а ограничение совместимости стимулов при низком уровне затрат R L — 3N L ≥ R H — 3N H, выполняются оба условия; в таком случае мы можем получить следующую цепочку неравенств (где мы учитывали тот факт, что значение N Hположительное):

R L — 3N L ≥ R H — 3N H ≥ 5N H — 3N H ≥ 5N H ≥ 0

Первое и последнее выражения цепочки неравенств говорят о том, что R L — 3N L ≥ 0. Поэтому нам нет необходимости отдельно рассматривать ограничение участия при низком уровне затрат 3N L≤ R L, так как оно удовлетворяется автоматически, когда удовлетворяются два оставшихся ограничения.

Кроме того, на интуитивном уровне очевидно, что компания, которая несет большие издержки, не заинтересована заявлять о себе как о компании с низкими издержками, поскольку тогда она получит меньшую оплату при более высоких затратах. Тем не менее этот интуитивный вывод требует проверки согласно строгой логике данного анализа. В связи с этим поступим следующим образом. Сначала исключим из рассмотрения второе ограничение совместимости стимулов, R H — 5N H ≥ R L — 5N L, что позволит решить задачу с двумя оставшимися ограничениями. Затем вернемся назад и убедимся в том, что решение задачи с двумя ограничениями удовлетворяет третьему ограничению, исключенному из рассмотрения. Иначе говоря, полученное решение должно также быть решением для задачи с тремя ограничениями. (При наличии более подходящего решения оно должно быть приемлемым и для задачи с меньшим количеством ограничений.)

Таким образом, нам остается проанализировать два ограничения: 5N H ≤ R Hи R L — 3N L ≥ R H — 3N H. Запишем их в таком виде: R H ≥ 5N Hи R L ≥ R H + 3(N L— N H). Обратите внимание, что цель правительства — сделать значения R Lи R H настолько малыми, чтобы они были совместимы с указанными выше ограничениями. Такой результат можно получить, представив каждое ограничение в виде равенства. В связи с этим примем такие равенства: R H = 5N Hи R L = R H + 3(N L— N H) = 3N L + 2N H. Теперь эти выражения для платежей по контракту можно подставить в формулу целевой функции G . В результате имеем

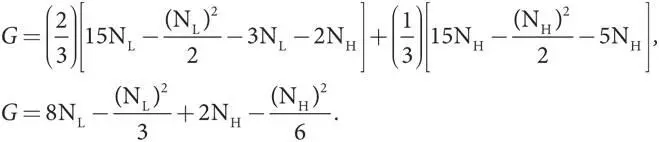
Целевая функция состоит из двух частей: одна (первые два члена) содержит только N L, а вторая (вторые два члена) только N H. Мы можем применить формулу максимизации отдельно к каждой части. В части N L A = 0, B = 8 и C = 1/3, а значит, оптимальное значение N L = 8/(2×1/3) = 24/2 = 12. В части N H A = 0, B = 2 и C = 1/6, стало быть, оптимальное значение N H = 2/(2×1/6) = 12/2 = 6.

Теперь можем использовать оптимальные значения N Lи N H, чтобы получить оптимальные значения платежей (R), воспользовавшись формулами для R Lи R H, выведенными выше. Подстановка в них N L = 12 и N H = 6 дает нам R H = 5 × 6 = 30 и R L = 3 × 2 + 2 × 6 = 48. Таким образом, мы имеем оптимальные значения для всех неизвестных в целевой функции правительства. Но не забывайте, что мы исключили из рассмотрения одно из ограничений совместимости стимулов, поэтому теперь нам необходимо к нему вернуться.

Мы должны убедиться, что третье ограничение, R H — 5N H ≥ R L — 5N L, согласуется с вычисленными нами значениями R и N. На самом деле так и есть. Левая сторона выражения равна 30 — 5 × 6 = 0, а правая — 48 — 5 × 12 = –12, а значит, ограничение действительно удовлетворяется.

Наше решение говорит о том, что органам власти штата нужно предложить следующих два контракта: «Контракт L: мы заплатим вам 48 миллиардов долларов за строительство 12 полос» и «Контракт H: мы заплатим вам 30 миллиардов долларов за строительство 6 полос». Как мы можем интерпретировать это решение, чтобы лучше понять его на интуитивном уровне? Интуитивное обоснование наиболее очевидно, если сравнить полученное решение с идеальным решением, найденным в разделе 3.Апри наличии полной информации о затратах. На рис. 13.2 представлены данные, позволяющие сопоставить оптимальные значения N и R.

Рис. 13.2.Значения показателей в контракте на строительство автомагистрали

Существует два важных различия между оптимальным механизмом в случае асимметричной и полной информации. Во-первых, хотя контракт, который целесообразно выбрать при условии низких затрат, подразумевает строительство такого же количества полос (12), что и при наличии полной информации, оплата по нему больше в асимметричном случае (48 вместо 36). Во-вторых, в случае асимметричной информации и высокого уровня затрат контракт подразумевает строительство меньшего количества полос (6 вместо 10), но обеспечивает такую же оплату, как и во втором варианте (30 = 6 × 5). Эти различия позволяют разделить типы.

В случае асимметричной информации у подрядчика может возникнуть соблазн сделать вид, будто он несет высокие затраты, тогда как на самом деле они низкие. Механизм оптимальной оплаты включает в себя как «пряник» для правдивого признания низких затрат, так и «кнут» за попытку симуляции высоких. «Пряник» — это сверхприбыль в размере 48–36 = 12, которую подрядчик заработает в результате косвенного признания низких затрат посредством выбора контракта L. «Кнут» — сокращение сверхприбыли от контракта H за счет уменьшения количества полос, которые будут при этом построены. Идеальный механизм оплаты при высоком уровне затрат подразумевает строительство 10-полосной автомагистрали за 50 миллиардов долларов; подрядчик с низким уровнем затрат заработал бы на таком контракте 50 — 3 × 10 = 20 миллиардов долларов. Оптимальный контракт с ограниченной информацией подразумевает строительство только шести полос, за что подрядчик получает 30 миллиардов долларов. Если истинный уровень затрат низкий, подрядчик заработает сверхприбыль в размере 30 — 3 × 6 = 12 миллиардов долларов. Следовательно, в этом случае он получит меньшую выгоду от завышенного уровня затрат (косвенно вытекающего из выбора подрядчиком контракта H, хотя его истинные затраты низкие). В действительности эта выгода сокращается ровно на величину, которую гарантирует часть механизма, соответствующая «прянику», что сводит на нет желание подрядчика завысить уровень издержек.

У рассмотренных выше механизмов есть одно общее свойство: агент владеет определенной частной информацией (в главе 8мы определили этот тип игрока). Кроме того, принципалу нужно, чтобы агент выполнил определенное действие, направленное на ее раскрытие. В терминах из главы 8эти механизмы представляют собой примеры скрининга в целях разделения типов посредством самоотбора.

Такие механизмы встречаются повсюду. Самые распространенные — механизмы ценовой дискриминации. Пока клиент готов заплатить сумму, превышающую предельные издержки компании на поставку соответствующего продукта, компания может получить прибыль за счет работы с данным клиентом. Однако его готовность платить может быть относительно низкой по сравнению с готовностью других потенциальных покупателей. Если компания должна установить одну и ту же цену всем своим клиентам, в том числе и тем, кто готов платить больше данного клиента, назначение ему цены в соответствии с его готовностью платить означает, что компании придется пожертвовать частью потенциальной прибыли от более платежеспособных клиентов. В идеале компания хотела бы прибегнуть к ценовой дискриминации, предоставив скидку клиентам с меньшей готовностью платить и не предлагая ее тем, кто готов платить больше.