Авинаш Диксит - Стратегические игры

Игру на рис. 14.4можно решить обычным способом. Мы уже видели, что на верхнем пути СССР, будучи сторонником жесткого курса, проигнорирует угрозу США, а на нижнем подчинится их требованиям в случае выполнения условия эффективности. Если это условие не будет удовлетворено, Советский Союз обоих типов проигнорирует угрозу Соединенных Штатов, поэтому им целесообразно вообще ее не выдвигать. В связи с этим будем исходить из предположения, что Советский Союз подчинится требованиям Соединенных Штатов, и проанализируем имеющиеся у США варианты выбора. По сути, вопрос состоит в следующем: насколько рискованной может быть угроза Соединенных Штатов, оставаясь при этом приемлемой?

Если США выдвинут угрозу, они с вероятностью p рискуют столкнуться с Советским Союзом, который придерживается жесткого курса, а значит, проигнорирует ее. При этом ожидаемый выигрыш США составит (–2–8 q ), как было вычислено выше. Вероятность того, что США будут иметь дело с СССР, поводящим мягкий курс, равна (1 — p ). Мы исходим из того, что тогда Советский Союз подчинится требованиям Соединенных Штатов и они получат выигрыш 1. Следовательно, их ожидаемый выигрыш от вероятностной угрозы при условии, что она окажется эффективной в противостоянии с СССР, равен

(–2–8 q ) × p + 1 × (1 — p ) = –8 pq — 3 p + 1.

Если Соединенные Штаты воздержатся от угрозы, их выигрыш составит −2. Стало быть, они могут выдвигать угрозу при выполнении следующего условия:

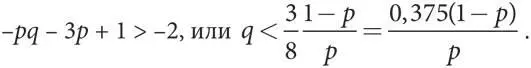
Иными словами, вероятность войны должна быть достаточно низкой, чтобы удовлетворять этому условию, или США лучше вообще такую угрозу не выдвигать. Мы называем этот верхний предел значений q условием приемлемости. Обратите внимание, что p входит в формулу максимального значения q , которое будет приемлемым для Соединенных Штатов: чем выше вероятность того, что СССР не уступит, тем меньше риск взаимной катастрофы, который США считают приемлемым.

Для того чтобы вероятностная угроза обеспечила требуемый результат, она должна удовлетворять как условию эффективности, так и условию приемлемости. Мы можем определить приемлемый уровень вероятности войны с помощью рис. 14.5. На горизонтальной оси отображены значения вероятности p того, что СССР придерживается жесткого курса, а на вертикальной — вероятность q того, что разразится война, если Советский Союз проигнорирует угрозу США. Горизонтальная линия q = 0,6 отображает нижний предел условия эффективности: угроза должна быть такой, чтобы связанная с ней точка ( p, q ) находилась над этой линией, если США имеют дело с СССР, который проводит мягкий курс. Кривая q = 0,375(1 — p )/ p дает верхний предел условия приемлемости: угроза должна быть такой, чтобы точка с координатами ( p, q ) находилась под этой линией, если предполагается, что угроза должна быть приемлемой для США даже в случае мягкого курса Советского Союза. Таким образом, эффективная и приемлемая угроза должна располагаться где-то между этими двумя линиями, сверху и слева от их пересечения в точке с координатами p = 0,38 и q = 0,6 (на рис. 14.5 эта область выделена серым).

Рис. 14.5.Условия успешного балансирования на грани

Эта линия достигает значения q = 1, когда p = 0,27. При всех p меньше этого значения серьезная угроза (неизбежность войны) приемлема для США и эффективна против СССР, придерживающегося мягкого курса. Это подтверждает выводы, сделанные по результатам анализа в разделе 3.

При всех значениях p в диапазоне от 0,27 до 0,38 серьезная угроза с вероятностью q = 1 смещает точку ( p, q ) направо от линии, отображающей условие приемлемости, и является слишком большой, чтобы быть приемлемой для США. Однако здесь можно найти угрозу меньшего масштаба. В данном диапазоне значений q некоторые значения достаточно низкие, чтобы быть приемлемыми для Соединенных Штатов, но в то же время достаточно высокие, чтобы принудить Советский Союз подчиниться. Балансирование на грани (с использованием вероятностной угрозы) позволяет в данном случае добиться поставленной цели, тогда как простая угроза была бы слишком рискованной.

Если значение p превышает 0,38, нет ни одного значения q , удовлетворяющего обоим условиям. Если вероятность того, что СССР не уступит, превышает 0,38, то любая угроза, достаточно большая для того, чтобы быть эффективной против Советов с мягким курсом ( q ≥ 0,6), создает чересчур высокий, а значит, неприемлемый для США риск войны. Следовательно, если p ≥ 0,38, США не поможет использование стратегии балансирования на грани.

Если Кеннеди располагает достаточно точной оценкой вероятности p того, что Советский Союз — сторонник жесткого курса, а также если он уверен в своей способности контролировать риск q того, что блокада приведет к ядерной войне, то у него есть возможность рассчитать и реализовать свою наилучшую стратегию. Как мы видели в разделе 3, если p < 0,27, серьезная угроза неизбежной войны приемлема для Кеннеди (даже если он решит использовать наименьшую эффективную угрозу, а именно при q = 0,6). Если значение p попадает в диапазон от 0,27 до 0,38, то Кеннеди должен прибегнуть к балансированию на грани. Такая угроза должна содержать в себе риск катастрофы 0,6 < q < 0,375(1 — p )/ p ; в этом случае Кеннеди тоже выберет наименьшее значение в данном диапазоне, то есть q = 0,6. При p > 0,38 Кеннеди следует уступить.

В действительности Кеннеди не знает точного значения p ; у него есть только приблизительная оценка того, что оно находится в диапазоне от 1/3 до 1/2. К тому же он не может быть уверен в точном местоположении критического значения q по отношению к графику условия приемлемости. Это зависит от чисел, используемых в качестве выигрышей Советского Союза при разных исходах (например, −8 в случае войны и −4 в случае выполнения требований США), Кеннеди может только приблизительно оценить эти значения. И наконец, он может даже не иметь возможности достаточно точно контролировать риск, возникший в связи с балансированием на грани. Все эти неопределенности говорят лишь об одном: нужна предельная осторожность.

Предположим, Кеннеди считает, что p = 0,35, и выдвигает угрозу, подкрепленную действием, которое несет в себе риск q = 0,65. Этот риск больше, чем необходимо, чтобы угроза была эффективной, а именно q = 0,6. Предел приемлемости составляет 0,375 × (1–0,35)/0,35 = 0,7, а риск q = 0,65 меньше этого предела. То есть, по подсчетам Кеннеди, такой риск удовлетворяет как условию эффективности, так и условию приемлемости. Но представим, что Кеннеди ошибается. Скажем, если он не осознает, что Лемей действительно может не выполнить приказы и предпринять чрезмерно агрессивные действия, то значение q может оказаться выше, чем его оценивает Кеннеди, например равным 0,8, что Кеннеди посчитал бы слишком рискованным. Или, допустим, значение p на самом деле равно 0,4; тогда Кеннеди счел бы даже q = 0,65 рискованным. Кроме того, эксперты Кеннеди могли бы неправильно оценить выигрыши Советского Союза. Если бы они оценили его унижение вследствие вывода ракет в −5, а не −4, то предельное значение условия эффективности составляло бы q = 0,7, поэтому угроза Кеннеди при q = 0,65 не достигла бы требуемой цели.