Дмитрий Елисеев - Рассказы о математике с примерами на языках Python и C

И наконец, перейдем к формулам вычисления Пи, т. к. именно в них можно увидеть красоту числовых взаимосвязей — то, чем интересна математика.

Формула Лю-Хуэя (3й век):

Формула Мадхавы-Лейбница (15 век):

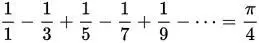
Формула Валлиса (17 век):

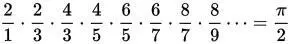
Формула Мэчина (18 век):

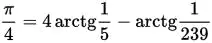
Попробуем вычислить число Пи по второй формуле. Для этого напишем простую программу на языке Python:

sum = 0.0

sign = 1

for p in range(0,33):

sum += 4.0 * sign / (1 + 2 * p)

print(p, sum)

sign = -sign

Запустим программу в любом онлайн-компиляторе языка Питон (например https://repl.it/languages/python3). Получаем результат:

Шаг Значение

0 4.0

1 2.666666666666667

2 3.466666666666667

3 2.8952380952380956

4 3.3396825396825403

5 2.9760461760461765

6 3.2837384837384844

7 3.017071817071818

8 3.2523659347188767

9 3.0418396189294032

10 3.232315809405594

11 3.058402765927333

12 3.2184027659273333

13 3.0702546177791854

14 3.208185652261944

15 3.079153394197428

16 3.200365515409549

17 3.0860798011238346

18 3.1941879092319425

19 3.09162380666784

20 3.189184782277596

21 3.0961615264636424

22 3.1850504153525314

23 3.099944032373808

24 3.1815766854350325

25 3.1031453128860127

26 3.1786170109992202

27 3.1058897382719475

28 3.1760651768684385

29 3.108268566698947

30 3.1738423371907505

31 3.110350273698687

32 3.1718887352371485

Как можно видеть, сделав 32 шага алгоритма, мы получили лишь 2 точных знака. Видно, что алгоритм работает, но количество вычислений весьма велико. Как известно, в 15-м веке индийский астроном и математик Мадхава использовал более точную формулу, получив точность числа Пи в 11 знаков:

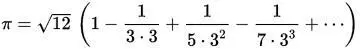
Попробуем воспроизвести ее в виде программы, чтобы примерно оценить объем вычислений.

Первым шагом необходимо вычислить √12. Возникает резонный вопрос — как это сделать? Оказывается, уже в Вавилоне был известен метод вычисления квадратного корня, который сейчас так и называется «вавилонским». Суть его в вычислении √S по простой формуле:

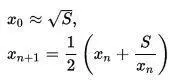
Здесь x0 — любое приближенное значение, например для √12 можно взять 3.

Запишем формулу в виде программы:

from decimal import Decimal

print ("Квадратный корень:")

number = Decimal(12)

result = Decimal(3)

for p in range(1, 9):

result = (result + number / result)/Decimal(2)

difference = result**2 - number

print (p, result, difference)

sqrt12 = result

Результаты весьма интересны:

Результат: √12 = 3,464101615137754

Как можно видеть, сделав всего 4 шага, можно получить √12 с достаточной точностью, задача вполне посильная даже для ручных расчетов 15 века.

Наконец, запрограммируем вторую часть алгоритма — собственно вычисление Пи.

sum = Decimal(1)

sign = -1

for p in range(1,32):

sum += Decimal(sign) / Decimal((2 * p + 1)*(3**p))

sign = -sign

print(p, sqrt12 * sum)

print("Result:", sqrt12 * sum)

Результаты работы программы:

Шаг Значение

1 3.079201435678004077382126829

2 3.156181471569954179316680000

3 3.137852891595680345522738769

4 3.142604745663084672802649458

5 3.141308785462883492635401088

6 3.141674312698837671656932680

7 3.141568715941784242161823554

8 3.141599773811505839072149767

9 3.141590510938080099642754230

10 3.141593304503081513121460820

11 3.141592454287646300323593597

12 3.141592715020379765581606212

13 3.141592634547313881242713430

14 3.141592659521713638451335328

15 3.141592651733997585128216671

16 3.141592654172575339199092210

17 3.141592653406165187919674184

18 3.141592653647826046431202391

19 3.141592653571403381773710565

20 3.141592653595634958372427485

21 3.141592653587933449530974820

22 3.141592653590386522717511595

23 3.141592653589603627019680710

24 3.141592653589853940610143646

Уже на 24-м шаге мы получаем искомые 11 знаков числа Пи. Задача явно требовала больше времени чем сейчас, но вполне могла быть решена в средние века.

Современные формулы не столь просты внешне, зато работают еще быстрее. Для примера можно привести формулу Чудновского:

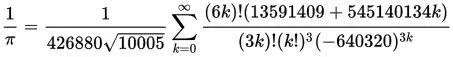
Для сравнения, те же 24 итерации по этой формуле дают число Пи со следующей точностью:

3.141592653589793238462643383279502884197169399375105820974944592307816406286208998628034825342117067982148086513282306647093844609550582231725359408128481117450284102701938521105559644622948954930381964428810975665933446128475648233786783165271201909145648566923460348610454326648213393607260249.

Если сделать 100 итераций и вычислить 1000 знаков Пи, то можно увидеть так называемую «точку Фейнмана»:

3.14159265358979323846264338327950288419716939937510582097494459230781640628620899862803482534211706798214808651328230664709384460955058223172535940812848111745028410270193852110555964462294895493038196442881097566593344612847564823378678316527120190914564856692346034861045432664821339360726024914127372458700660631558817488152092096282925409171536436789259036001133053054882046652138414695194151160943305727036575959195309218611738193261179310511854807446237996274956735188575272489122793818301194912983367336244065664308602139494639522473719070217986094370277053921717629317675238467481846766940513200056812714526356082778577134275778960917363717872146844090122495343014654958537105079227968925892354201995611212902196086403441815981362977477130996051870721134 9999998372978049951059731732816096318595024459455346908302642522308253344685035261931188171010003137838752886587533208381420617177669147303598253490428755468731159562863882353787593751957781857780532171226806613001927876611195909216420207

Это последовательность «999999», находящаяся на 762-м знаке от начала. Желающие могут поэкспериментировать дальше самостоятельно с помощью программы на языке Python:

from math import factorial

from decimal import *

def chudnovsky(n):

pi = Decimal(0)

k = 0

while k < n:

pi += (Decimal(-1)**k) * (Decimal(factorial(6 * k)) / ((factorial(k)**3) * (factorial(3*k))) * (13591409 + 545140134 * k) / (640320**(3 * k)))

k += 1

print("Шаг: {} из {}".format(k, n))

pi = pi * Decimal(10005).sqrt() / 4270934400

pi = pi**(-1)

return pi

# Требуемая точность (число знаков)

N = 1000

getcontext().prec = N

val = chudnovsky(N / 14)

print(val)

Эта программа не оптимизирована, и работает довольно-таки медленно, но для ознакомления с сутью алгоритма этого вполне достаточно. Кстати, с помощью формулы Чудновского два инженера Александр Йи и Сингеру Кондо в 2010 году объявили о новом мировом рекорде вычисления Пи на персональном компьютере: 5 трлн знаков после запятой. Компьютеру с 12 ядрами, 97 Гб памяти и 19 жесткими дисками потребовалось 60 дней для выполнения расчетов.