Дмитрий Елисеев - Рассказы о математике с примерами на языках Python и C
- Название:Рассказы о математике с примерами на языках Python и C
- Автор:
- Жанр:
- Издательство:неизвестно
- Год:неизвестен
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Дмитрий Елисеев - Рассказы о математике с примерами на языках Python и C краткое содержание
Книга распространяется бесплатно, скачать оригинал в PDF можно на странице
.
Рассказы о математике с примерами на языках Python и C - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
#include
#include
#include
#include
bool isPerfect(unsigned long long int n)
{
unsigned long long int sum = 1, i;
for(i=2; i<=sqrt(n)+1; i++)
{
if (n%i==0) {
sum += i;
if (i != n/i) {
sum += n/i;
}
}
}
return sum == n;
}
int main()
{
unsigned long long int n = 137438691328LL;
bool res = isPerfect(n);
printf("%d\n", res);
return 0;
}
Компилируем программу с помощью компилятора gcc, запускаем получившийся exe-файл: время выполнения меньше секунды, уже гораздо лучше. Теперь несложно поменять функцию main для перебора всех чисел от 1 до 200000000000. В код также добавлен вывод промежуточных результатов каждые 1000000 итераций, чтобы видеть ход выполнения программы.
int main()
{
unsigned long long int MAX = 200000000000LL;
unsigned long long int p;
for (p=1; p
if (isPerfect(p))
printf(" %llu ", p);
if (p % 1000000 == 0)
printf("*%llu,%llu*", 100*p/MAX, p);
}
}
Увы, прогноз относительно скорости расчетов оказался слишком оптимистичным. Примерно за час работы программы, было перебрано лишь 100 млн. вариантов, а для перебора всех 200 млрд. понадобился бы не один день. Желающие могут продолжить процесс самостоятельно, однако с уверенностью можно сказать что в диапазоне от 1 до 100000000 действительно нет совершенных чисел кроме 6, 28, 496, 8128 и 33550336.
Проверка числа 2 305 843 008 139 952 128 является непростой задачей даже для современного домашнего компьютера — во-первых, в языке C/C++ нет встроенных типов данных для столь большого числа, а во-вторых, число вариантов перебора весьма велико.
Разумеется, выше было приведено самое простое решение «в лоб», можно оптимизировать и саму программу, например разбить вычисление на несколько процессорных ядер, однако данная задача выходит за рамки этого материала. Немного про параллельные вычисления будет рассказано в конце книги.
7. Магический квадрат
Еще одна старинная математическая головоломка — магический квадрат. Магическим называют квадрат, заполненный неповторяющимися числами так, что суммы чисел по горизонталям, вертикалям и диагоналям одинаковы. Такие квадраты известны давно, самым старым из известных является магический квадрат Ло Шу, изображенный в Китае в 2200 г. до нашей эры. Если подсчитать количество точек, то можно перевести квадрат в современный вид, изображенный справа.
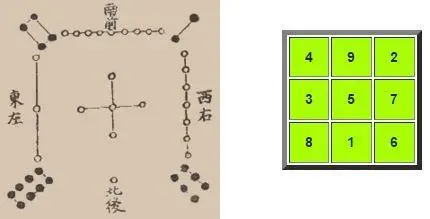
Магический квадрат 4х4 был обнаружен в индийских надписях 11 века:

И наконец, известный квадрат 4х4, изображенный на гравюре немецкого художника Дюрера «Меланхолия». Этот квадрат изображен не просто так, 2 числа 1514 указывают на дату создания гравюры.

Как можно видеть, уже математики прошлого умели строить магические квадраты разной размерности. Интересно рассмотреть их свойства.
Сумма чиселмагического квадрата размера NxN зависит только от N, и определяется формулой:
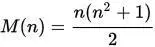
Это несложно доказать, т. к. сумма всех чисел квадрата равна сумме ряда 1..N 2. Действительно, для квадрата Дюрера M(4) = 34, что можно посчитать на картине. Для квадратов разной размерности суммы равны соответственно: M(3) = 15, M(4) = 34, M(5) = 65, M(6) = 111, M(7) = 175, M(8) = 260, M(9) = 369, M(10) = 505.
Напишем программу для построения магических квадратов размерности N. Первый подход будет «в лоб», напрямую. Создадим массив, содержащий все числа от 1 до N 2и получим все возможные перестановки этого массива. Их число довольно-таки велико, и составляет 1 * 2 * .. * N = N! вариантов. Также для каждого массива необходимо проверить, является ли он «магическим», т. е. выполняется ли требование равенства сумм.
Для получения всех перестановок воспользуемся алгоритмом, описанным здесь — https://prog-cpp.ru/permutation/.
Код программы приведен ниже:
def swap(arr, i, j):
arr[i], arr[j] = arr[j], arr[i]
def next_set(arr, n):
j = n - 2
while j != -1 and arr[j] >= arr[j + 1]: j -= 1
if j == -1:
return False
k = n - 1
while arr[j] >= arr[k]: k -= 1
swap(arr, j, k)
l = j + 1
r = n – 1
while l < r:
swap(arr, l, r)
l += 1
r -= 1
return True
def is_magic(arr, n):
for i in range(0, n):
sum1 = 0
sum2 = 0
sum3 = 0
sum4 = 0
for j in range(0, n):
sum1 += arr[i * n + j]
sum2 += arr[j * n + i]
sum3 += arr[j * n + j]
sum4 += arr[(n – j - 1) * n + j]
if sum1 != sum2 or sum1 != sum3 or sum1 != sum4 or sum2 != sum3 or sum2 != sum4 or sum3 != sum4:
return False
return True
def show_squares(n):
N = n * n
arr = [i + 1 for i in range(N)]
cnt = 0
while next_set(arr, N):
if is_magic(arr, n):
print(arr)
cnt += 1
return cnt
# Требуемая размерность
cnt = show_squares(3)
print("Число вариантов:", cnt)
Программа выдала 8 вариантов для N = 3, время вычисления составило 2 секунды:
| [2, 7, 6, 9, 5, 1, 4, 3, 8] | [6, 1, 8, 7, 5, 3, 2, 9, 4] |
| [2, 9, 4, 7, 5, 3, 6, 1, 8] | [6, 7, 2, 1, 5, 9, 8, 3, 4] |
| [4, 3, 8, 9, 5, 1, 2, 7, 6] | [8, 1, 6, 3, 5, 7, 4, 9, 2] |
| [4, 9, 2, 3, 5, 7, 8, 1, 6] | [8, 3, 4, 1, 5, 9, 6, 7, 2] |
Действительно, как известно, существует только 1 магический квадрат 3x3:
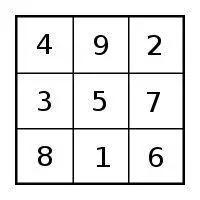
Остальные являются лишь его поворотами или отражениями (очевидно что при повороте квадрата его свойства не изменятся).
Теперь попробуем вывести квадраты 4х4. Запускаем программу… и ничего не видим. Как было сказано выше, число вариантов перебора для 16 цифр равняется 16! или 20922789888000 вариантов. На моем компьютере полный перебор такого количества занял бы 1089 дней!
Однако посмотрим на магический квадрат еще раз:
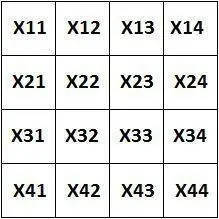
Суммы всех элементов по горизонтали и вертикали равны. Из этого мы легко можем записать равенство его членов:
x11 + x12 + x13 + x14 = x21 + x22 + x23 + x24 x11 + x12 + x13 + x14 = x14 + x24 + x34 + x44 x11 + x12 + x13 + x14 = x13 + x23 + x33 + x43 x11 + x12 + x13 + x14 = x12 + x22 + x32 + x42 x11 + x12 + x13 + x14 = x11 + x21 + x33 + x44 x11 + x12 + x13 + x14 = x31 + x32 + x33 + x34
И наконец, общая сумма: т. к. квадрат заполнен числами 1..16, то если сложить все 4 строки квадрата, то получаем 4S = 1 + .. + 16 = 136, т. е. S = 34 (что соответствует приведенной в начале главы формуле).
Читать дальшеИнтервал:
Закладка:









