Дмитрий Елисеев - Рассказы о математике с примерами на языках Python и C
- Название:Рассказы о математике с примерами на языках Python и C
- Автор:
- Жанр:
- Издательство:неизвестно
- Год:неизвестен
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Дмитрий Елисеев - Рассказы о математике с примерами на языках Python и C краткое содержание
Книга распространяется бесплатно, скачать оригинал в PDF можно на странице
.
Рассказы о математике с примерами на языках Python и C - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
‐ Другое известное изображение — спираль Фибоначчи, которая строится по похожему принципу соотношения размеров прямоугольников:
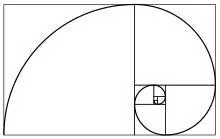
Это изображение также часто встречается в природе, от раковин моллюсков, до формы атмосферного циклона или даже спиральной галактики.
Для примера достаточно взять фотографию циклона из космоса, и наложить обе картинки вместе:
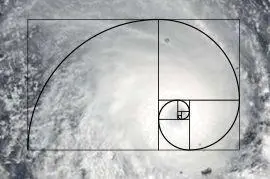
‐ Если взять и разделить друг на друга 2 любых соседних члена последовательности, например 233/377, получится число 0,618. Случайно это или нет, но это число — то самое «золотое сечение», считающееся наиболее эстетичной пропорцией.
Числа Фибоначчи несложно вывести в программе на языке Python:
from decimal import *
def printNumbers(n):
i1 = Decimal(0)
i2 = Decimal(1)
for p in range(1, n+1):
print("F({}) = {}".format(p, i2))
fib = i1 + i2
i1 = i2
i2 = fib
getcontext().prec = 100
N = 100
printNumbers(N)
Интересно заметить, что растет последовательность Фибоначчи весьма быстро, уже
F(300) = 222232244629420445529739893461909967206666939096499764990979600.
10. Высота звуков нот
Еще в древности человек заметил, что натянутая струна порождает колебания звука. Во времена Пифагора было замечено, что струны издают мелодичный звук, если их длина соотносится как небольшие целые числа (1:2, 2:3, 3:4 и т. д.). Звук от струны длиной 2/3 дает чистую квинту, 3/4 струны дает кварту а половина струны — октаву.
Рассмотрим струну с условной длиной = 1. Будем умножать длину струны на 3/2, если полученное число больше 2, разделим еще на 2.
1.
3/2 = 1,5
1.5 * 3/2 = 2.25, 2.25/2 = 1,125 = 9/8
9/8 * 3/2 = 1,6875 = 27/16
Похожий ряд, если его упорядочить по возрастанию, называется пифагоровым строем:
«до» — 1
«ре» — 9/8
«ми» — 81/64
«фа» — 4/3
«соль» — 3/2
«ля» — 27/16
«си» — 243/128
«до» — 2
Он также называется квинтовым, т. к. ноты получались увеличением на квинту, т. е. на 3/2. Считается, что этот строй использовался еще при настройке лир в древней Греции, и сохранился вплоть до средних веков. Названия нот разумеется, были другие — современные названия придумал только через 1000 лет итальянский теоретик музыки Гвидо д’Ареццов 1025 г.
Разумеется, в древней Греции никто не знал про частоту колебаний звука, зато древние греки были хорошими геометрами, и проблем с умножением и делением у них не было. Современная теория колебаний струны появилась гораздо позже, работы Эйлераи Д’Аламберабыли написаны в 1750-х годах.
Как математически определяются частоты звуков нот? Сейчас мы знаем, что октава (от «до» до «до» следующей октавы) — это умножение частоты на 2 (или укорочение струны в 2 раза). Для остальных нот с 18 века используется так называемый «хорошо темперированный строй»: октава делится на 12 равных промежутков, а последовательность частот образует геометрическую прогрессию.
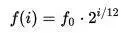
Для одной октавы получаются следующие коэффициенты: 1,0594, 1,1224, 1,1892, …, 2. На клавиатуре они отображаются всем известным образом, образуя 12 полутонов:
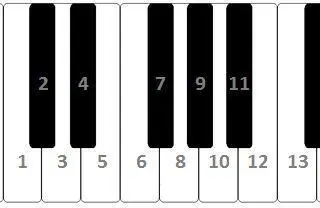
Таким образом, если знать частоту любой ноты, все остальные легко рассчитываются по вышеприведенной формуле.
Очевидно, что «базовая» частота может быть любой. Традиционно принято например, что частота камертона ноты «Ля» 440 Гц. Остальные ноты первой октавы:
| ДО | 261.6 | ДО# | 277 |
| РЕ | 293.7 | РЕ# | 311 |
| МИ | 329.6 | ||
| ФА | 349.2 | ФА# | 370 |
| СОЛЬ | 392 | СОЛЬ# | 415 |
| ЛЯ | 440 | ЛЯ# | 466 |
| СИ | 494 |
Интересно заметить, что квинта в этой системе имеет соотношение частот 2 7/12= 1,49, что чуть-чуть отличается от «пифагорейского» чистого тона с соотношением 1.5. На слух «современная квинта» имеет небольшие биения 0,5 Гц, соответствующие разности частот 392—392,4. До сих пор есть любители исполнения старинной музыки в квинто-терцевом строе, называемым «чистым». В 18-м же веке дебаты между приверженцами «старого» и «нового» строя были довольно-таки острыми. Впрочем, преимущества равномерно темперированного строя в виде четкого соотношения между частотами нот и возможности транспонирования музыки в любую другую тональность «без потери качества» оказались решающими. Сейчас «чистый строй» имеет лишь историческое значение, и используется лишь иногда для исполнения старинных произведений.
И традиционно, программа на языке Python, выводящая частоты полутонов в обе стороны от ноты «Ля»:
import math
freqLa = 440
for p in range(-32, 32):
freq = freqLa * math.pow(2, p / 12.0)
print p,freq
11. Вращение планет
Еще в древней Греции ученые знали, что планеты движутся по небу, но каким образом? Сотни лет господствовала геоцентрическая система мира — в центре была Земля, вокруг которой по окружностям двигались Луна, планеты (на то время их было известно 5) и Солнце:
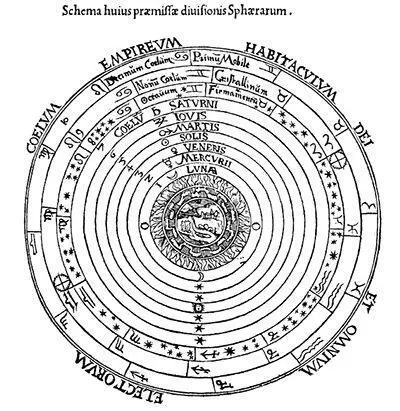
Такая система казалась вполне логичной и интуитивно понятной (даже сейчас люди говорят что солнце «всходит» и «заходит»), однако не объясняла астрономам почему планеты движутся по небу неравномерно, и временами даже в обратную сторону.
Вот так, к примеру, выглядит перемещение по небу планеты Марс, что никак не укладывается в теорию движения по кругу:
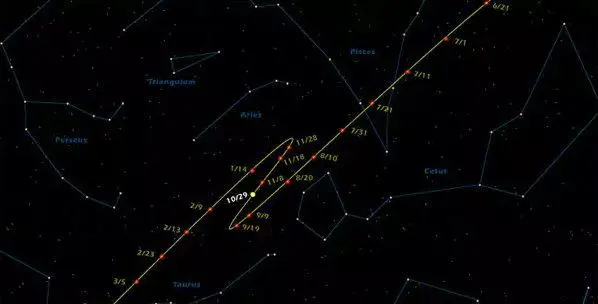
Впрочем геоцентрическая система просуществовала более 1500 лет, только в 16-м веке Коперник издал свой труд «О вращениях небесных сфер», где описывал вращение планет по круговым орбитам вокруг Солнца. Однако проблемой было то, что и при этой схеме фактические движения планет не совпадали с расчетными.
Объяснить это не мог никто, пока в 1600 году немецкий математик Иоганн Кеплер не стал изучать многолетние результаты наблюдений, сделанные астрономом Тихо Браге. Кеплер был великолепным математиком, но и у него ушло несколько лет чтобы понять суть и вывести законы, которые и сейчас называются законами Кеплера.
Как оказалось, движение планет подчиняется 3-м математическим законам:
1) Планеты движутся по эллиптическим орбитам, в одном из фокусов эллипса находится Солнце:
Читать дальшеИнтервал:
Закладка:









