Виталий Сигорский - Математический аппарат инженера

Однако теория графов как математическая дисциплина сформировалась только к середине тридцатых годов нашего столетия благодаря работам многих исследователей, наибольшая заслуга среди которых принадлежит Д. Кенигу. Значительный вклад в теорию графов внесли советские ученые Л. С. Понтрягин, А. А. Зыкоз, В. Г. Визинг и др.

Теория графов располагает мощным аппаратом решения прикладных задач из самых различных областей науки и техники. Сюда относятся, например, анализ и синтез цепей и систем, проектирование каналов связи и исследование процессов передачи информации, построение контактных схем и исследование конечных автоматов, сетевое планирование и управление, исследование операций, выбор оптимальных маршрутов и потоков в сетях, моделирование жизнедеятельности и нервной системы живых организмов, исследование случайных процессов и многие другие задачи. Теория графов тесно связана с такими разделами математики, как теория множеств, теория матриц, математическая логика и теория вероятностей. Во всех этих разделах графы применяют для представления различных математических объектов, и в то же время сама теория графов широко использует аппарат родственных разделов математики.

2. Ориентированные графы.Часто связи между объектами характеризуются вполне определенной ориентацией. Например, на некоторых улицах допускается только одностороннее автомобильное движение, в соединительных проводах электрической цепи задаются положительные направления токов, отношения между людьми могут определяться подчиненностью или старшинством. Ориентированные связи характеризуют переход системы из одного состояния в другое, результаты встреч между командами в спортивных состязаниях, различные отношения между числами (неравенство, делимость).

Для указания направления связи между вершинами графа соответствующее ребро отмечается стрелкой. Ориентированное таким образом ребро называют дугой, а граф с ориентированными

- 46 -

ребрами - ориентированным графом или короче орграфом (рис. 8, а).

Если пара вершин соединяется двумя или большим числом дуг, то такие дуги называют параллельными. При этом две дуги, одинаково направленные по отношению к данной вершине, называют строго параллельными, а различно направленные — нестрого параллельными. Ясно, что нестрого параллельные дуги, отображающие ориентацию связи в обоих направлениях, по существу равноценны неориентированной связи и могут быть заменены ребром. Произведя такую замену в орграфе, придем к смешанному графу, который содержит ребра н дуги (рис. 8, б). Обратно, любой неориентированный или смешанный граф можно преобразовать в ориентированный заменой каждого ребра парой нестрого параллельных дуг.

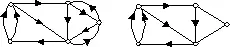
Рис. 8. Ориентированный (а) и смешанный(б) графы.

Изменив направления всех дуг орграфа на противоположные, получаем орграф, обратный исходному. Если направления дуг орграфа не учитываются и каждая дуга рассматривается как неориентированное ребро, то он называется соотнесенным (неориентированным) графом.

3. Взвешенные графы. Дальнейшее обобщение отображения связей между объектами с помощью графов состоит в приписывании ребрам и дугам некоторых количественных значений, качественных признаков или характерных свойств, называемых весами.

В простейшем случае это может быть порядковая нумерация ребер и дуг, указывающая на очередность при их рассмотрении (приоритет или иерархия). Вес ребра или дуги может означать длину (пути сообщения), пропускную способность (линии связи), напряжение или ток (электрические цепи), количество набранных очков (турниры), валентность связей (химические формулы), количество рядов движения (автомобильные дороги), цвет проводника (монтажная схема электронного устройства), характер отношений между людьми (сын, брат, отец, подчиненный, учитель) и т. п.

Вес можно приписывать не только ребрам и дугам, но и вершинам. Например, вершины, соответствующие населенным пунктам на карте автомобильных дорог, могут характеризоваться количеством мест в кемпингах, пропускной способностью станций техобслуживания. Вообще, вес вершины означает любую характеристику соответствующего ей объекта (атомный вес элемента в структурной формуле, цвет изображаемого вершиной предмета, возраст человека и т. п.).

- 47 -

Особое значение для моделирования физических систем приобрели взвешенные ориентированные графы, названные графами потоков сигналов или сигнальными графами. Вершины сигнального графа отождествляются с некоторыми переменными, характеризующими состояние системы, а вес каждой вершины означает функцию времени или некоторые величины, характеризующие соответствующую переменную (сигнал вершины). Дуги отображают связи между переменными, и вес каждой дуги представляет собой численное или функциональное отношение, характеризующее передачу сигнала от одной вершины к другой (передача дуги). Сигнальные графы находят широкое применение в теории цепей и систем, а также во многих других областях науки и техники.

4. Типы конечных графов.Если множество вершин графа конечно, то он называется конечным графом. В математике рассматриваются и бесконечные графы, но мы заниматься ими не будем, так как в практических приложениях они встречаются редко. Конечный граф G = (V, E), содержащий р вершин и q ребер, называется (р, q)-графом.

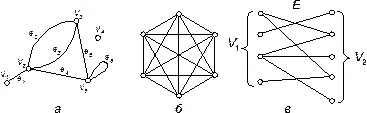
Рис. 9. Типы графов:

а - псевдограф; б - полный граф (шестиугольник); в - двудольный граф (биграф).

Пусть V = { v 1, v 2, ..., v p} и E = { e 1, e 2, ..., e q} - соответственно множества вершин и ребер (р, q)-графа. Каждое ребро e k∈ E соединяет пару вершин v i∈ V являющихся его концами (граничными вершинами). Для ориентированного ребра (дуги) различают начальную вершину, из которой дуга исходит, и конечную вершину, в которую дуга заходит. Ребро, граничными вершинами которого является одна и та же вершина, называется петлей. Ребра с одинаковыми граничными вершинами являются параллельными и называются кратными. В общем случае граф может содержать и изолированные вершины, которые не являются концами ребер и не связаны ни между собой, ни с другими вершинами. Например, для (5, 6)-графа на рис. 9, а V={ v 1, v 2, v 3, v 4, v 5}; Е= {e 1, e 2, e 3, e 4, e 5} ребра e 2и e 3параллельны, ребро e 6является петлей, а v 4- изолированная вершина.

- 48 -

Число ребер, связанных с вершиной v i(петля учитывается дважды), называют степенью вершины и обозначают через δ(v i) или deg (v i). Так, для графа на рис. 9, а δ(v 1) =1, δ(v 2) = 4 и т. д. Очевидно, степень изолированной вершины равна нулю δ(v 4) = 0). Вершина степени единицы называется концевой или висячей вершиной ( δ(v 1) =1). Легко показать, что в любом графе сумма степеней всех вершин равна удвоенному числу ребер, а число вершин нечетной степени всегда четно. В орграфе различают положительные δ +(v i) и отрицательные δ -(v i) степени вершин, которые равны соответственно числу исходящих из v iи заходящих в v iдуг. Например, для вершины d орграфа (см. рис. 9, а) имеем δ +(d) = 2 и δ -(d) = 3. Очевидно, суммы положительных и отрицательных степеней всех вершин орграфа равны между собой и равны также числу всех дуг.